błąd w książce ? ekstremum olo33: wyznacz ekstremum : f(x)==arcsin e^x według mnie niema ekstremum ale w odpowiedziach jest i teraz mam taki mętlik Df=(−∞;0> y''= e^x/√1−e^x wke : y'=0 e^x=0 niema takiego x ∊R

Adamm: −1≤e^x≤1 x≤0

	ex
y'=		>0, dziedzina pochodnej: x<0
	√1−ex

ponieważ funkcja jest rosnąca to mamy ekstremum dla x=0, ekstremum to miejsce dla którego w otwartym otoczeniu punktu mamy wartości mniejsze (większe) od tego punktu

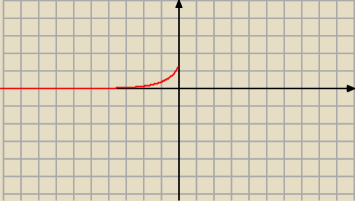
olo33: teraz jak patrze na wykres to widzę , ale co z warunkiem koniecznym istnienia ekstremum lokalnego y'=0 ? Pan to z doświadczenia zauważył a jak to wyliczyć/ zauważyć

Adamm: y'=0 jest warunkiem koniecznym istnienia ekstremum jeśli funkcja jest różniczkowalna (ma pochodną), oczywiście na przedziale otwartym jeśli nie ma (tak jak w przypadku 0) może się zdarzyć że mamy w tym miejscu ekstremum też jeśli funkcja jest różniczkowalna na domkniętym przedziale to może się zdarzyć że na jednym z końców tego przedziału istnieje ekstremum nawet jeśli y'≠0

olo33: Rozumiem, dziękuje panu