Proszę o pomoc Ela : Ile jest liczb czterocyfrowych w których zapisie występują tylko cyfry od 1 do 6 i które zawierają w swoim zapisie conajmniej jedna piątkę i co najmniej jedna czwórkę..?

Adamm:

4 1	4 1
		*6*6 = 576

Adamm:

4 1	3 1
		*62 = 432

Aga.1.: odp 432. jest prawidłowa.

Ela : Czy tyle samo jest możliwych wyników 4 rzutkow sześcienna kostka w których pojawia sie 4 i 5 przynajmniej raz ?

Ela : Jest mi to potrzebne w zadaniu na prawdopodobieństwo

Adamm: jeszcze raz, źle napisałem wszystkich jest 6⁴ bez piątki jest 5⁴ bez czwórki jest 5⁴ z bez piątki i czwórki jest 4⁴ 6⁴−(5⁴+5⁴−4⁴)=1296−994=302

Adamm: Ela tyle samo

Ela : Czyli prawdopodobieństwo wyrzucenia co najmniej jednej piątki pod warunkiem ze wypadła co najmniej jedna czwórka wynosi 432/671?Czy dobrze myśle ?

Adamm:

	302		151
raczej		=
	1296		648

Mila: Dobrze 20:19

Adamm: Mila, czemu? możesz rozwiązać to zadanie?

Ela : To jak w końcu mam z tego sprawdzian w poniediedzialek i nic nie umiem

Mila: Może niech Ela, napisze oryginalną treść zadania, bo są tu różne wersje.

Ela : Oblicz prawdopodobieństwo ze w czterokrotnym rzucie sześcienna kostka do gry wypadnie jedna piątka pod warunkiem ze wypadła jedna czwórka?

Adamm: ahh, pod warunkiem

Ela : Nie wiem skąd bierze sie to 302, przecież na 4 sposoby umieszczam piątkę na 3 czwórkę i na dwa pozostałe miejsca od 1 do 6 dowolnie wiec wychodzi 432 , nie wiem gdzie jest błąd w myśleniu?

Mila: Czyli nie ma w treści: "co najmniej" ?

Mila: Elu wcześniej podałaś zupełnie inną treść zadania.

Mila: Czy to jest takie zadanie? http://www.zadania.info/d616/514432

Ela : Przepraszam

Ela : Tak to to zadanie ale wgl nie rozumiem rozwiązania

Mila: Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej jedną „czwórkę”, pod warunkiem że otrzymamy co najmniej jedną „piątkę”. |Ω|=6⁴ A− otrzymamy co najmniej jedną „czwórkę”, B− otrzymamy co najmniej jedną „piątkę”. A∩B− otrzymamy co najmniej jedną piątkę i co najmniej jedną czwórkę. |B|=6⁴−|B'| B' − nie otrzymamy ani jednej piątki |B'|=5⁴ tworzymy ciągi 4 wyrazowe o wartościach ze zbioru {1,2,3,5,6} |B|=6⁴−5⁴=671 na tyle sposobów otrzymamy co najmniej jedną piątkę rozpisuję dokładnie: |A∩B| Mamy takie zdarzenia : 1) dokładnie jedna piątka 54XY − 4*3* 4²=192 − 4− wybór miejsca dla piatki 3− wybór miejsca dla czwórki pozostałe ze zbioru: {1,2,3,6}

	4 1		3 2
544x −		*		*4=48

5444− 4 możliwości 2) dokładnie dwie piątki

	4 2
554x −		*2*4=48

	4!
5544−		=6
	2!*2!

3) dokladnie 3 piątki 5554 − 4 możliwości ===== suma |A∩B|=192+48+4+48+6+4=302

	302
P(A/B)=
	671

=========== Teraz pytaj czego nie rozumiesz.

Eta:

	|A∩B|
P(A/B)=
	|B|

|B|=6⁴−5⁴= 671 i jak napisał Adamm |A∩B|= 6⁴−(5⁴+5⁴−4⁴)= 302

	302
P(A/B)=
	671

Ela: A czy nie mogę po prostu na 4 sposoby wybrać miejsca dla czwórki, na 3 dla piątki i na pozostałe po 6 ponieważ mogą sie powtarzać?

Mila: Spróbuj zrobić po swojemu , liczba zdarzeń sprzyjających ma się zgadzać. Wypisałam na piechotę, abyś " widziała" te zdarzenia, ale liczebność zdarzeń w A∩B lepiej zrobić tak, jak Adam. Czy rozumiesz ten sposób? Skorzystaj ze zdarzenia (A∩B)'.

Ela: Czy dopełnienie iloczynu zbiorów A i B wynosi 4⁴ ? Tzn takie w których nie występuje 4 i 5 czyli 4 możliwości na każde miejsce ?

Ela: Ale wtedy wychodzą kompletne głupoty

Ela: Czy wie ktos skąd to sie bierze ?

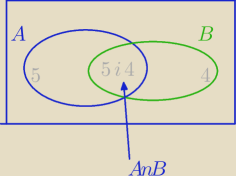
Mila: (A∩B)'=A'∪B' |A'∪B'|=|A'|+|B'|−|A'∩B'| Tam na rysunku odwrotnie 5 z 4. |A'|=5⁴ cyfry ze zbioru {1,2,3,5,6} ( bez 4) |B'|=5⁴ cyfry ze zbioru {1,2,3,4,6} (bez 5) |A'∩B'|= 4⁴ cyfry ze zbioru {1,2,3,6} (bez4 i bez 5) teraz licz.

Ela: Dziękuje

Mila: Już jasne? Popatrz na rysunek i zastanów się co w tych zbiorach jest, i co poza zbiorami.