Oblicz sumę pierwiastków równania należących do przedziału <0, 6π> Ola: Oblicz sumę pierwiastków równania należących do przedziału <0, 6π> a) sin x = 1/2 b) cos x = −1/2 c) sin x = 0.9

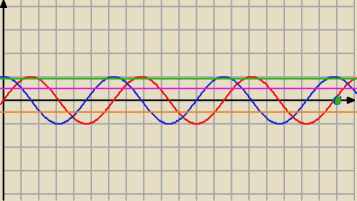
Adamm: a) 6 b) 6 c) 6

Adamm: przepraszam, odczytałem "ilość pierwiastków"

Ola: Odpowiedzi w książce mam takie: a) 15π b) 18π c) 15π

Adamm: sinα=1/2 α∊(0;π/2), również sin(π−α)=1/2, etc. a) (α+π−α)+(α+π−α+4π)+(α+π−α+8π)=15π

Adamm: b) cosα=−1/2, α∊(π/2;π), również cos(−α+2π)=−1/2 etc. (α−α+2π)+(α−α+2π+4π)+(α−α+2π+8π)=18π

Adamm: c) analogicznie do a)

Ola: Skąd się bierze to α=(0; π/2)? Skąd jest to π/2

Adamm: z rysunku na przykład, chciałem pokazać jedynie że to nie jest równanie, tylko za α biorę konkretną wartość