Geometria analityczna Fran: Mam problem z następującymi trzema zadaniami: 1. Punkt K jest środkiem ciężkości trójkąta ABC, gdzie A(1, −9), B(7, 6), C(−2, 12). Wyznacz wektor CK. 2.Dany jest punkt E(0, 2) i prosta p: y= −4. Wszystkie punkty płaszczyzny, których odległość od punktu E jest równa odległości od prostej p, należą do paraboli. Wyznacz ją. 3. Obrazem okręgu o: (x−2)² + y² = 3, w przekształceniu P określonym wzorem P((x,y)) = (2x − 1, 4 − 2y), gdzie x, y ∊ R, jest okrąg o środku S i promieniu r. Wyznacz ten okrąg.

Alky: Odnośnie 1 jest chociażby wzór na środek ciężkości trójkąta ( jest w kartach, sory jestem leniwy ) potem tylko wektor z 1 punktu do 2 to ez Do 3 mnożysz x i y przez przekształcenie i zamieniasz znowu na rówanianie okręgu i widać wszystko ładnie 2 aż dam się oszaleć i zrobię bo mam przeryty beret i ledwo rozumiem co tu jest napisane

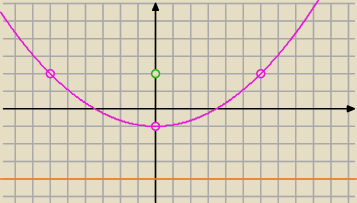
===: 2)