Znaleźć równania normalne i parametryczne płaszczyzny: Miś: Witam mam takie polecenie jak w tytule i taki podpunkt przechodzącej przez punkt A = (−2, 5, 4) oraz prostopadłej do osi Oy. nie mogę sobie wyobrazić rysunku tej płaszczyzny. Policzyć umiem, potrzebuję trzy punkty dwa wektory i liczę normalne a parametryczne jeden punkt dowolny i dwa wektory

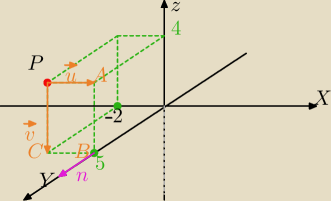
Mila: A = (−2, 5, 4) 1) [0,1,0] − wektor kierunkowy osi OY jest wektorem normalnym szukanej płaszczyzny 0*(x+2)+1*(y−5)+0*(z−4)=0 π: y−5=0 − równanie ogólne płaszczyzny 2) równanie parametryczne np. takie: u^→=[2,0,0] v^→=[0,0,−4] x=−2+2t+0s y=5+0t+0s z=4+0t−4s s,t∊R Krócej: x=−2+2t y=5 z=4−4s ======

Miś: y−5=0 to chyba równanie normalne płaszczyzny?

Mila: Na to wygląda. Wyszło od razu, bez potrzeby normalizacji. N=√A²+B²+C²=√1=1 wsp. normalizacji

Miś: a jeszcze pytanko skąd się wzięły wektory u i v?

Mila: Zmieniłam oznaczenie. W poprzednim wpisie , źle zapisałam oznaczony punkt w układzie , ma być: P= (−2, 5, 4) to dany punkt To są wektory leżące w szukanej płaszczyźnie. A=(0,5,4) PA^→=[2,0,0] C(−2,5,0) PC^→=[0,0,−4]

Miś: Teraz rozumiem dziękuję

Mila: