Przekatne czworokata wypuklego ABCD przecinaja sie w punkcie P.Oblicz pole tego czworokata
wiedzac, ze pola trojkatow ABP, BCP, CDP sa rowne odpowiednio 3,4,5
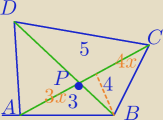ΔAPB i ΔPCB mają wspólną wysokość opuszczoną z wierzchołka B⇒
| AP | 3 | ||
= | |||
| PC | 4 |
| PΔAPD | 3x | ||
= | ⇔ | ||
| PΔPCD | 4x |
| PΔAPD | 3 | ||
= | ⇔ | ||
| 5 | 4 |
| 15 | ||
PΔAPD= | ||
| 4 |
| 15 | ||
PABCD=3+4+5+ | ||
| 4 |