moduł z parametrem Lolalolalo: Wyznacz wszystkie wartości parametru a dla których równanie ||x+2|−3|=a−x ma nieskończenie wiele rozwiązań. Podaj rozwiniecie dziesiętne ilorazu iloczynu znalezionych wartości przez ich sumę.

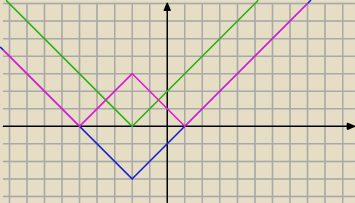
Jerzy: Fioletowy to wykres: ||x+2| − 3| Prosta: y = − x + a musi się z nim pokrywać.

Lolalolalo: Nie rozumiem...

Lolalolalo: Mogłabym prosić o obliczenia?

Jerzy: Czego ?

Jerzy: Obydwie proste muszą przechodzić przez II i IV ćwiartkę ( bo jest −x) Teraz tak dobierz a, aby te proste pokrywały się z odpowiednimi fragmentami fioletowej krzywej.

Lolalolalo: Ogólnie to całego zadania, nie wiem z którymi fragmentem ma się prosta pokrywać, jak zapisać obliczenia i drugiej części zadania.

Jerzy: Popatrz na wykres. Pierwsza prosta przechodzi przez punkty (−5,0) (−2,−3) Druga przez: (0,1) (1,1)

Lolalolalo: A nie da się tego zrobić bez wykresu? Niestety dla mnie to czarna magia.

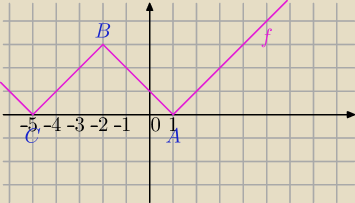
Mila: Graficzny sposób jest najłatwiejszy. f(x)=||x+2|−3| g(x)≥0⇔a−x≥0, interesuje nas gdzie wykres (g(x) pokrywa się z wykresem funkcji f(x) 1) g(x)=a−x − prosta o ujemnym wsp. kierunkowym więc może mieć część wspólną AB⇔ a=1 gdzie (0,1)− punkt przecięcia z OY g(x)=1−x dla x≥−2 i x≤1 lub 2) g(x) ma część wspólną dla x≤−5 g(−5)=0 ⇔a−(−5)=0⇔a=−5 g(x)=−5−x odp. a=1 lub a=−5 Metoda algebraiczna Za chwilę.

Mila: ||x+2|−3|=a−x a−x≥0⇔x≤a 1)|x+2|=x+2 dla x≥−2 wtedy mamy równanie: |x+2−3|=a−x |x−1|=a−x⇔ x−1=a−x lub x−1=−a+x pierwsze równanie może mieć tylko jedno rozw. a drugie : dla 1=a ma nieskończenie wiele rozwiązań, g(x)=1−x dla x≥−2 i 1−x≥0 ⇔x∊<−2,1> lub 2) |x+2|=−x−2 dla x≤−2 |−x−2−3|=a−x i a−x≥0⇔ −x−5=a−x lub −x−5=−a+x dla a=−5 równanie pierwsze ma nieskończenie wiele rozwiązań i −5− x≥0⇔x≤−5 g(x)=−5−x i x≤−5

Lolalolalo: Dziękuję bardzo ❤