wykres
olla:
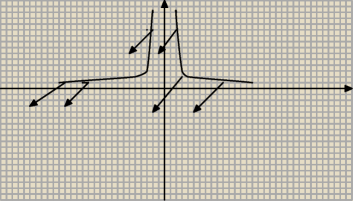
walczę z wykresami funkcji wymiernej czy dobrze to pojmuje.
| | 1 | |
narysuj wykres y=| |
| −3| |
| | |x|+2 | |
| | 1 | |
pierwszy etap to rysuje.y= |
| |
| | |x| | |
drugi etap to wektor (−2,−3) i myślę ze tu robie bład bo ciągnę obie hiperbole najpierw w lewo
o dwie jednostki, a potem do dołu o trzy
Mam nadzieję że widać o co chodzi, a potem powinnam to wszystko odbić nad oś X
ale nie zrobię tego bo wiem że na tym etapie to jest źle sprawdzałam sobie na tych programach
do rysowania i niestety mi tak nie wychodzi, co robię w tych przesunięciach wektorów źle ?
4 sty 19:30
olla: z tego co kombinowałam na tych stronach do rysowania wykresów to
wychodzi mi tak jakby jedną hipe ciągną w prawo , a drugą w lewo.
nie wiem czy wiecie o co mi chodzi−dlaczego tak się dzieje bo jest
wartość bezwzględna, pewnie mnie nie zrozumiecie o co chodzi bo jesteście ścisłowcami
ale miło by mi było
jakby ktos się wczytał o co mi chodzi w tym pytaniu
4 sty 19:33
yht:
2. Wektor (−2,−3)
3. Odbicie tego co na dole, do góry
4. Wartość bezwzględną na x
4 sty 19:43
olla: to wiem, pokaz jesi mozesz moment przesunięcia o wektor −2,−3
4 sty 19:47
yht:
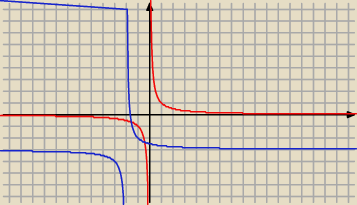
4 sty 19:48
olla: kurcze jednak i mi i tobie wychodzi źle
4 sty 22:11
===:
| | 1 | | 1 | |
musisz uzmysłowić sobie różnicę między f(x)= |
| i g(x)= |
| |
| | x | | |x| | |
4 sty 22:13
olla:
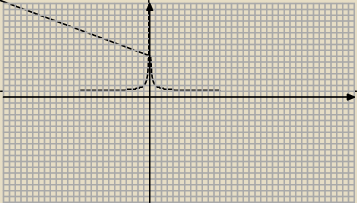
4 sty 22:17
olla:
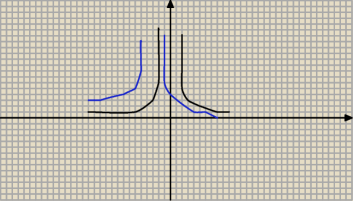
potem przesuwam o wektor −1
4 sty 22:23
===:
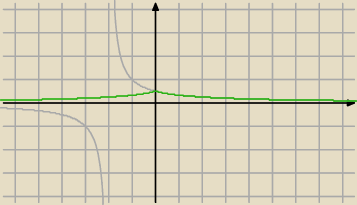
4 sty 22:24
===:
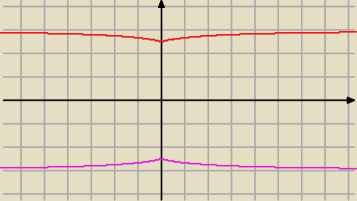
| | 1 | |
f(x)=| |
| −3| czerwony |
| | |x|+2 | |
4 sty 22:28
olla: czy dobrze idzie? z punktów wychodzi mi to tak bo nie umiem tego tu narysować
były punkty (1,1)(1/2, 2) (2, 1/2) a na lewo miałam punkty (−1,1)(−1/2,1)(−1,1/2) po
przesunięciu najpierw o −2 w lewo wyszły punkty
(−1,1)(−1,5 ,1) (0,1/2) w drugim wykresie (−3,1)(−1,5 ,1) (−3, 1/2) myslę ze tu coś mam nie
tak
4 sty 22:30
olla:

| | 1 | |
no własnie rozumiem siwy wykres i robie w ten sposób |
| stąd nie wyłazi w sumie wykres |
| | |x| | |
4 sty 22:36
olla: i potem przesuwam ten z lewej o o 2 w lewo i ten z prawej również o 2 w lewo więc czemu nie
wychodzi ten zielony?
4 sty 22:37
olla: dlaczego ten zielony tak się wypłaszczył

4 sty 22:38
===:
dlatego na wstępie napisałem że musisz ogarnąć różnicę a dokładniej jak powstaje wykres
funkcji gdzie argument jest pod modułem
4 sty 22:38
olla: ten argument będzie zawsze dodatni tak?
4 sty 22:41
olla: będzie w pierwszej i drugiej ćwiartce asymptoty to osie x i y
4 sty 22:42
olla: oczywiscie dodatnia y
4 sty 22:42
olla: kurcze zasadniczy moment w którym się gubię
4 sty 22:43
===:
zaraz mnie tu "zmyją" za język nie matematyczny

ale mówiąc po chłopsku f(|x|) to nie |f(x)|
4 sty 22:45
===:
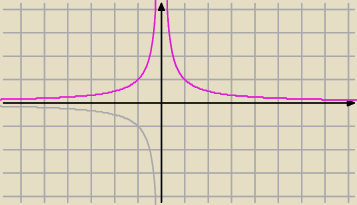
zauważ, że wykres
| | 1 | |
f(x)= |
| fioletowy powstaje nie przez odbicie trzeciej ćwiartki do góry |
| | |x| | |
ale poprzez odbicie prawej strony względem osi 0y
4 sty 22:49
olla: za pomoc nie nalezy nikogo "zmywać" siedzę w programie do rysowania i tam oczywiście wychodzi
tak jak tobie, próbuje tez sobie rozne punkty wstawiać ale widocznie dalej cos źle robię bo
nijaknie moge zalapac dlaczego ginie górna część tego zielonego wykresu
4 sty 22:50
olla: tak ja to rozumiem i zobacz ze moje brzydkie rysunki własnie tak jak ten fioletowy to maja
przedstawiać, ale problem zaczyna się gdy przesuwam w lewo o 2 i np punkt (1,1) ma wpółrzeddne
(−1,1) i teraz pytanie czy punkt (−1,) będzie mieć współrzedne (1,1) ? i tak mam robic z
kazdympunktem prawda ?
4 sty 22:53
===:
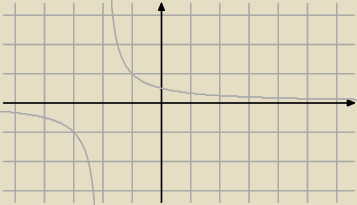
| | 1 | | 1 | |
na tym co powyżej jest to bez różnicy bo f(x)= |
| =| |
| | |
| | |x| | | x | |
| | 1 | |
ale dla f(x)= |
| to już różnica |
| | |x|+2 | |
4 sty 22:54
piotr: narysuj |1/(x+2)−3| dla x>0 i potem lustro względem OY
4 sty 22:58
===:
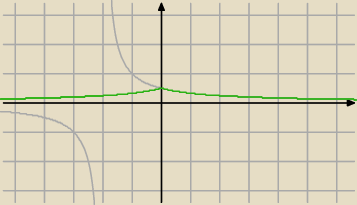
i teraz najważniejsze

| | 1 | | 1 | |
f(x)= |
| na prawo od 0y pozostaje jak dla f(x)= |
| |
| | |x|+2 | | x+2 | |
ale dla ujemnych argumentów nie odbijasz względem 0x ale "lustro" względem 0y
4 sty 23:00
piotr:
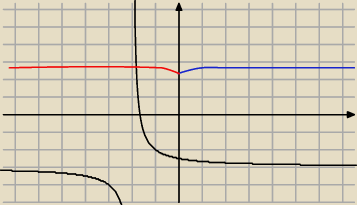
4 sty 23:02
olla: mój problem polega na tym, że siwy wykres rozumiem od "a" do "z"
nie rozumiem zielonego niestety skąd taki wypłaszczony ten zielony
4 sty 23:07
olla: piotr i tu to samo czarne rozumiem ale czerwony i niebieski znowu magia − wyję po prostu już
wyję że nie mogę tego dostzrec
4 sty 23:08
piotr: === źle narysował np. dla x=0 powinno być 2,5 a u === jest 0,5
4 sty 23:10
piotr: czarny to jest |1/(x+2)−3|, potem z tego biorę część dla x≥0 i odbijam względem OX i wychodzi
niebieski i dalej niebieski odbijam względem OY,
wykres to niebieski i czerwony łącznie
4 sty 23:13
piotr: poprawka: czarny to jest 1/(x+2)−3
4 sty 23:14
olla: myśle ze dobrze mówisz piotr bo mi tez wychodzi w tym programie 2,5 tym nie mniej próbuje
zrozumiec dlaczego taki płaski ten wykres
4 sty 23:15
===:
bo TY
piotr nie czytasz tylko wypisujesz bee
zauważ jaki wykres narysowałem (opis)
pełen wykres narysowałem uprzednio w poście z 22:28
potem krok po kroku usiłowałem wyjaśnic co i skąd
ale ty wcinasz się jak ...

4 sty 23:15
olla: źle interpretujesz w mianowniku x jest w module i na koniec wszystko w drugim module
4 sty 23:16
olla: to było oczywiście do piotra x w mianowniku jest w module
4 sty 23:16
piotr: ok === dopatrzyłem się tego późnie
4 sty 23:19
olla: ====mi to wyglada tak jakbym miala ten fioletowy czyli podstawowy wykres narysowany pzrze
ciebie ten z lewej przesunąc +2 w prawo a ten wykres z prawej −2 w lewo i wtedy coś niby
wychodzi ale nie można tak zmieniac wektora
4 sty 23:20
piotr: podana funkcja jest parzysta, więc rozpatruję |1/(x+2)−3| dla x≥0 i potem odbicie względem OY
i mam wykres dla x<0
4 sty 23:22
olla: mimo wszystko dziękuje wszytskim za pomocnie pozostało mi nic innego jak podziękować i pogodzić
się ze NIGDY NIGDY tego nie zrozumiem /chodzi o moduł/ bo bez modulu to zabawa. Mówią ze nie
chca sie uczyć, chcę ale co z tego jak jeszcez sie taki nie urodził co by mi to wytłumaczyl,
dzięki pała bedzie murowana
4 sty 23:22
===:
olla ...daj sobie spokój z tym wektorem

!
Czytaj co się do Ciebie pisze

4 sty 23:23
piotr: podaną funkcję możesz rozpisać tak:
|1/(−x+2)−3| dla x<0
|1/(x+2)−3| dla x≥0
4 sty 23:26
olla: | | 1 | |
==== własne wektor mi wszystko psuje narysowałeś tak ładnie ten fioletowy i to jest |
| i |
| | |x| | |
teraz o −2 w lewo ale niestety nie wyszło niby najprostsze, ale nie wychodzi.Ktoś musi dostac
pałe, żeby wypelnic dną statystyczna i to bede ja.
4 sty 23:27
olla: po czterech godzinach niczym urlich von Jugingen podaję się, dobranoc wszytskim i dzięi za
próbę pomocy. Widocznie nie umiem czytac ze zrozumieniem jak ponoć większość Polaków.
4 sty 23:29
===:
zatrzymasz się jeszcze moment?

4 sty 23:30
olla: powiem tak trzymając się wykresu twojego fioletowego jak robię prawą część wychodzi mi poprawie
połowa wykresu, ale z lewą częścią mam problem i tyle nie zrozumiem już tego
4 sty 23:36
olla: nawet jak odbiłam względem OY to co napisales nic nie wyszlo
4 sty 23:37
===:
bo |x| powoduje to, że lewa strona wykresu to lustrzane odbicie prawej strony
4 sty 23:38
olla:
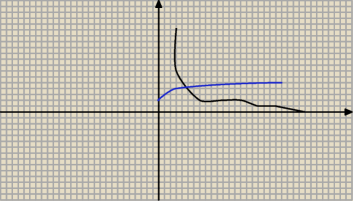
czarny wyjsciowy i potm wektory i wszytsko ok a lewa mrok
4 sty 23:39
olla: to znaczy ze teraz moge sobie ten niebieski odbic wzgledem OY na lewo i to juz wszystko
niby bedzie ok. Czyli tak jakby zawsze bezpieczniej zaczac od tego co ma argumenty na plusie i
potem na lewo odbić ?
,
4 sty 23:41
===:
otworzę nowy post ok

4 sty 23:41
kama: Ok ale to już i tak nic nie zmieni powiedz czy to co napisałam w ostadtnim poscie można zrobic
4 sty 23:44
===:
tak dokłądnie
4 sty 23:46
===:
piszemy tu?
4 sty 23:46
olla: dzięki, ale już wymiękłam.DZIĘKUJĘ za pomoc

4 sty 23:51
===:
| | 1 | |
zakładamy, że f(x)= |
| −3 |
| | x+2 | |
| | 1 | |
tedy rysujesz ją jako f(x)= |
| przesuniętą o wektor |
| | x | |
4 sty 23:53
yht:
nakładanie wartości bezwzględnej na samego "x" jest zawsze
końcowym przekształceniem
najlepiej po prostu wykuć na pamięć taką zasadę − zawsze działa
5 sty 09:08
 walczę z wykresami funkcji wymiernej czy dobrze to pojmuje.
walczę z wykresami funkcji wymiernej czy dobrze to pojmuje.


 potem przesuwam o wektor −1
potem przesuwam o wektor −1




 ale mówiąc po chłopsku f(|x|) to nie |f(x)|
ale mówiąc po chłopsku f(|x|) to nie |f(x)|
 zauważ, że wykres
zauważ, że wykres

 i teraz najważniejsze
i teraz najważniejsze 


 !
Czytaj co się do Ciebie pisze
!
Czytaj co się do Ciebie pisze

 czarny wyjsciowy i potm wektory i wszytsko ok a lewa mrok
czarny wyjsciowy i potm wektory i wszytsko ok a lewa mrok


 najlepiej po prostu wykuć na pamięć taką zasadę − zawsze działa
najlepiej po prostu wykuć na pamięć taką zasadę − zawsze działa