Pochodne Monika: Badając pochodne jednostronne rozstrzygnąć, czy istnieją pochodne podanych funkcji we wskazanych punktach: a) f(x) = min {x², 1}, x₀ = −1

Adamm: lim_x→−1⁻ min{x², 1} = lim_x→−1⁻ 1 = 1 lim_x→−1⁺ min{x², 1} = lim_x→−1⁺ x² = 1 f(−1)=1, funkcja jest ciągła w tym punkcie

	f(−1+Δx)−f(−1)		(−1+Δx)2−1
limΔx→0+		= limΔx→0+		= −2
	Δx		Δx

	f(−1+Δx)−f(−1)		1−1
limΔx→0−		= limΔx→0−		= 0
	Δx		Δx

pochodne stronne są różne

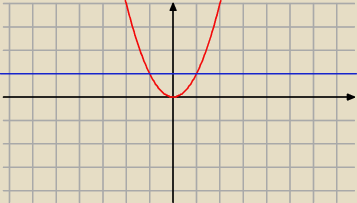
Adamm: można to przedstawić graficznie, już z rysunku widać że w punktach x=±1 funkcja nie ma pochodnych

Monika: Dzieki