Algebra JJ: Obliczyć odległość między prostymi skośnymi. l1: x = −1 + t, y = −1 + 2t, z = 2t; t∊R l2: x = s, y = −1 + 2s, z = 2 − 2s; s∊R Znalazłem wzór na obliczenie tej odległości d(l1,l2) = |(v1 x v2) o AB|/|v1 x v2| (nad wektorami v1, v2, AB oczywiście powinny być strzałeczki) i z tego wzoru otrzymuje poprawną odpowiedź. Wzór jak wzór ale może wylecieć z głowy na egzaminie dlatego wolę alternatywną drogę, tylko że wychodzi błędna odpowiedź i nie wiem gdzie leży problem. 1. Wyznaczam punkt należący do l1 czyli A(−1, −1, 0) oraz punkt leżący na l2 A'(s, −1 + 2s, 2 − 2s). 2. Wyznaczam wektor kierunkowy v prostej l2, czyli v = [1, 2, −2] 3. Liczę wektor AA' i rozwiązuje równanie AA' o v = 0 (iloczyn skalarny) 4. Z powyższego równania wyliczam s, dzięki czemu otrzymuje współrzędne rzutu punktu A na prostą l2 5. Obliczam długość wektora AA' i otrzymana długość jest odległością między tymi prostymi O ile ten sposób w przypadku prostych równoległych zdaje egzamin o tyle przy prostych skośnych wychodzi niepoprawny wynik.

Mila: Napisz jaka jest odpowiedź. Pomogę.

JJ: Według książki i pierwszego sposobu ze wzorem 2/√5 natomiast tym drugim sposobem wychodzi mi 2

Mila: Już piszę.

Mila: l₁,l₂− proste skośne (sprawdziłam) k₁^→=[1,2,2]− wektor kierunkowy prostej l₁ k₂^→=[1,2,−2]−wektor kierunkowy prostej l₂ P₁=(−1,−1,0)∊l₁ P₂=(0,−1,2)∊l₂ Piszemy równanie płaszczyzny π równoległej do obu prostych n^→=[1,2,2] x [1,2,−2]=[−8,4,0] wektor normalny szukanej pł. uprościmy rachunki: [−8,4,0] || [2,−1,0] P₁∊π π : 2*(x+1)−1*(y+1)=0 π: 2x−y+1=0 Obliczamy odległość P₂ od pł. π

	I2*0−1*(−1)+1|		2
d(P2,π)=		=
	√22+1		√5

====================

JJ: Dziękuję bardzo. Większość już zrozumiałem jednak nie mogę sobie wyobrazić jak to możliwe, że istnieje płaszczyzna równoległa do obu prostych mimo, że one same względem siebie nie są równoległe. Odnośnie zapisu P1∊π rozumiem, że możemy również wyznaczyć płaszczyznę w której zawarty jest punkt P2 zamiast P1 i obliczyć odległość punktu P1 od płaszczyzny π ?

Mila: Weź dwie krawędzie skośne w Twoim pokoju ( poziomą w podłodze i pionową), czy widzisz płaszczyznę równoległą ? Jeśli nie widzisz to spróbuję coś narysować.

Mila: Tak . Masz napisane równanie płaszczyzny zawierającą prostą l₁, w ten sam sposób możesz napisać równanie zawierającą prostą l₂ ( ten sam wektor normalny) i liczyć odległość płaszczyzn z wzoru. Spróbuj to zrobić. Jeśli znajdę inny sposób , to napiszę, więc zerknij tu jeszcze.

JJ: Nie widzę nadal tej płaszczyzny równoległej

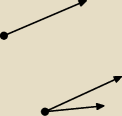
jc: JJ, masz dwa punkty w których wystają wektory kierunkowe prostych. Przesuń równolegle drugi z tych wektorów do miejsca, z którego wystaje pierwszy. Teraz rozepnij na tych wektorach płaszczyznę (wektory te mają różne kierunki, bo proste nie są równoległe). To będzie właśnie płaszczyzna równoległa do obu prostych.

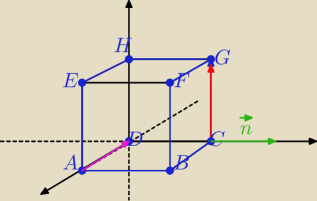
Mila: AD i CG − krawędzie skośne BCGF i ADHE płaszczyzny równoległe zawierające te krawędzie.

JJ: Super, dziękuję Panu/Pani jc i Pani Milu za świetne wyjaśnienia. Teraz w końcu będę w stanie sobie to wyobrazić

Mila: Powodzenia.

Jerzy: Ja nadal optuję za najprostszą metodą.... objętość rownolegloscianu podzielona przez pole jego podstawy.

jc: Jerzy, w zupełności się z tobą zgadzam. Jedno spojrzenie i wszystko jasne.