płaszczyzny Karolcia:

	x−3		y+4		z−2
Napisać równanie płaszczyzny zawierającej prostą		=		=		i równoległej
	2		1		−3

do prostej x=−5+4t, y=2+7t, z=2+t. Punkt z równania prostej w której ona sie zawiera to P(3,−4,2) Wektor normalny N[2,1,−3] Poza tym wydaje mi sie ze to powinno być równoległa do płaszczyzny wektor normlany tej drugiej to [4,7,1] nie wie co dalejz tym zrobić

Jerzy: Szukana płaszczyzna przechodzi przez punkt P(3,−4,2) , a jej wektor normalny jest prostopadły do wektora kierunkowego podanej prostej.

Jerzy: Nie tak ... Wektorem normalnym szukanej płaszczyzny jest iloczyn wektorowy tych dwóch prostych.

Jerzy: oczywiście iloczyn wektorowy ich wektorów kierunkowych.

Karolcia: czyli znalezc wektor kierunkowy tej drugiej prostej tak?

Karolcia: okej juz sie zagubiłam w tym, nie rozumiem

Jerzy: Tak, potem ich iloczyn i masz wektor normalny płaszczyzny i punkt , więc napiszesz równanie.

Jerzy: v₁ − wektor kierunkowy jednej prostej v₂ − wektor kierunkowy drugiej prostej n^→ = v₁ x v₂

Jerzy: n^→ = [2,1,−3] x [4,7,2] oraz P(3,−4,2)

Jerzy: [4,7,1] oczywiście.

jc: Kierunki prostych: (2,1,−3) (4,7,1) Wektor do nich prostopadły (11,−7,5) Równanie szukanej prostej 11(x−3)−7(y+4)+5(z−2)=0

Karolcia: wymnirzone te dwa wektory to [22,14,10]

Jerzy: [22,−14,10]

Karolcia: na pewno −14? skad to sie wzieło?

Jerzy: = [(1 + 21) , (−12 − 2) , (14 − 4)] = [22,−14,10]

Karolcia: a tam nie jest 2−(−12)?

Jerzy: Nie jest.

Jerzy: jc podał ten sam wektor...obaj się mylimy ?

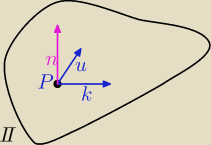
Mila: k→⁼[2,1,−3] u^→[4,7,1] n^→=[2,1,−3] x [4,7,1]=[22,−14,10] || [11,−7,5] π: 11(x−3)−7*(y+4)+5*(z−2)=0 11x−7y+5z−71=0 Tak, jak Panowie obliczyli

Jerzy: Witam i pozdrawiam

Mila: Też pozdrawiam, wszystkiego najlepszego w nowym roku

Karolcia: nie, po prostu zapomniałam, że zmieniamy znak przy drugiej liczbie, przepraszam i dziękuję

Kacper: