Granica
Oros: Granice(oblicz) :
Czy mógłby ktoś to ładnie rozpisać ? Nie wychodzi mi tutaj kompletnie nic w tym przykładzie,
mimo że wydaje się być łatwy.
3 sty 23:38
Oros: Pomoże ktoś ?
3 sty 23:55
Jack:
| | x | | √x2 | | x2 | |
lim |
| = lim |
| = lim √ |
| = √−1 = √i2 = −i ? |
| | √1−x2 | | √1−x2 | | 1−x2 | |
x−>
∞
| | x | | −√x2 | | x2 | |
lim |
| = lim |
| = lim − √ |
| = −√−1 = −√i2=i ? |
| | √1−x2 | | √1−x2 | | 1−x2 | |
x−> −
∞
jakos tak
4 sty 00:07
Jack: nie, cos pomieszalem.
4 sty 00:10
Janek191:
x ∊ ( − 1, 1)
4 sty 00:11
Janek191:
Granice w nieskończoności nie mają sensu.
4 sty 00:15
Jack: wg wolframa wynosza " − i " oraz " i "
4 sty 00:19
Oros: | | x | |
To w jaki sposób mam sprawdzić asymptoty funkcji f(x) = |
| ? |
| | √1−x2 | |
4 sty 00:20
Jack: po prostu ich tam nie ma
4 sty 00:22
Jack: mam na mysli + i − ∞
co do −1 i 1 to mozesz
4 sty 00:22
Jack: przy czym to co chcesz obliczyc to nie obliczysz?
mozesz obliczyc −1 prawostronne oraz 1 lewo, ale tak jak Ty chcesz, to nie obliczysz.
to juz urojone granice : D
4 sty 00:26
Oros: Więc mają sens, bo wynik udowadnia brak asymptoty. Aha, czyli pomyliłem kierunki przy −1 i 1 ?
4 sty 00:27
Janek191:
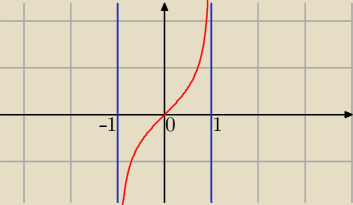
4 sty 00:29
Jack:
−1 prawostronne
1 lewostronne
policz.
4 sty 00:32
Oros: Dzięki, zabieram się za lizcenie − za jakieś 10 min podeślę wynik, więc jeśli będziesz mógł to
sprawdź.
4 sty 00:44
Jack:
| | x | | −1 | |
lim |
| = |
| = − ∞ |
| | √(1−x)(1+x) | | 0+ | |
x−> −1
+
| | x | | 1 | |
lim |
| = |
| = ∞ |
| | √(1−x)(1+x) | | 0+ | |
x−> 1
−
4 sty 00:48
Oros: Dziękuję.
4 sty 00:52
Oros: Ostatnie czego potrzebuję na ten moment, a nie chcę zakładać tematu.
Jeżeli miałem polecenie, żeby znaleźć styczną do krzywej y=
√x*e
−√x w dowolnym punkcie
x0>0 to czy moje rozwiązanie jest prawidłowe ?
http://imgur.com/a/wdys4
Tutaj zdjęcie obliczeń
4 sty 00:56
Jack: jest ok.
chociaz (co do samego zapisu)
zamiast tylu nawiasow to mozna by zapisac
| 1 | | e− √x(1−√x) | |
| * e − √x(1−√x) jako po prostu |
| |
| 2√x | | 2√x | |
ale ogolnie jest

4 sty 01:02
Oros: Dzięki wielkie, zawsze miałem problem ze stycznymi i dlatego wolałem się upewnić, a że tak
powiem mój zapis do najładniejszych nie wygląda więc czułem się niepewnie.
4 sty 01:03
Jack: znaczy chwilka, tam zamiast x jest wszedzie x0
bo obliczyles pochodna, ale pochodna w danym punkcie to wspolczynnik kierunkowy stycznej
4 sty 01:05
Oros: Jedynie w 2 nawiasie (końcowy wynik) powinien zostać x−x0, prawda ?
4 sty 01:07
Jack: czyli ostatecznie
| | e− √x0 (1−√x0) | |
y = |
| (x−x0) + √x0 * e− √x0 |
| | 2√x0 | |
4 sty 01:08
Jack: tak,
a teraz zycze dobrej nocy !

4 sty 01:14
Oros: Dokładnie tak, dziękuję i również życzę spokojnej nocy.
4 sty 01:15


