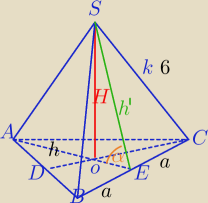
Pilne ! Paula: w ostrosłupie prawidłowym trójkątnym krawędz boczna ma długość 6 cm a kąt pomiędzy ścianą boczną a płaszczyzną podstawy wynosi 30 stopni. oblicz pole całkowite, objętość, pole siany bobocznej, wysokość ostrosłupa, krawędz podstawy, przekątną podstawy, pole podstawy i kąt pomiędzy ścianami bocznymi

Mila: To chyba Twoja twórczość ? Trójkąt nie ma przekątnej. α=30^o |AB|=|BC|=|AC|=2a 1) W ΔSEC: 6²=a²+h'² a²+h'²=36

	1		1		2a√3		a√3
2) |OE|=		h=		*		=
	3		3		2		3

	OE
cos30o=
	h'

√3		OE		√3		a√3		√3
	=		⇔|OE|=		*h'⇔		=		*h'⇔
2		h'		2		3		2

	2a
h'=
	3

=====

	2a
3)a2+(		)2=36
	3

	18
a=
	√3

	36
|AB|=
	√13

==========

	36		12
4)h'=		=
	3*√13		√13

Pole jednej ściany bocznej:

	1		1		36		12		216
PBCS=		*2a*h'=		*		*		=
	2		2		√13		√13		13

5) pole podstawy

	(2a)2√3		324√3
PΔABC=		=a2*√3=
	4		13

6) P_c oblicz sama 7) Wysokość ostrosłupa W ΔSOE:

	H
sin30o=
	h'

1		H
	=
2		h'

2H=h'

	2a
2H=
	3

	a
H=
	3

	18		6
H=		=
	3*√3		√13

	1
8) V=		*PΔABC*H oblicz sama
	3

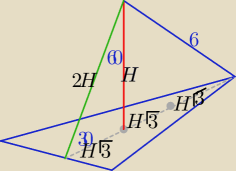Eta: Można uprościć obliczenia wykorzystując własność "trójkąta ekierki" o kątach 30^o,60^o,90^o:

	6		12
H2+(2H√3)2=36 ⇒ 13H2=36 ⇒ H=		to hb=2H=
	√13		√13

a√3		36
	=H√3 ⇒ a=6H=
6		√13

P_p=3H*3H√3= 9H²√3=.... P(ściany)= 3H*2H=6H²=...

	1
V=		*Pp*H = 3H3√3=.....
	3