Dowód Jack: Jak udowodnić, że x ≤ e^x−1 ?

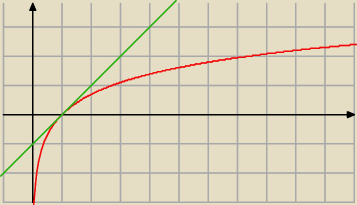
g: ln(x) ≤ x−1 Dla x=1 zachodzi: 1) ln(1) = 1−1, oraz 2) ln'(x) = (x−1)', więc te dwa wykresy są styczne Druga pochodna ln(x) jest zawsze ujemna, więc ln(x) ≤ x−1. Funkcja ln(x) jest rosnąca, więc x ≤ e^x−1.

Adamm: e^x−1−x=f(x) f'(x)=e^x−1−1 x=1 jest ekstremum tej funkcji, a dokładniej minimum f(1)=0 stąd f(x)≥0 czyli e^x−1≥x

Jack: g nie rozumiem zapisu ln'(x) = (x−1)' Adamm to, ze funkcja ma minimum dla x = 1 swiadczy o tym, ze f(x) ≥ 0?

Jack: a tak ogolnie to dzieki !

Adamm: tak bo jest to minimum globalne

Jack: a, to ze cos jest ekstremum globalnym nie trzeba pokazac, za pomoca granic w + − ∞ ?

Adamm: funkcja maleje dla x<1 i rośnie dla x>1, to że x=1 jest minimum globalnym jest już oczywiste

Adamm: i oczywiście funkcja jest ciągła

Jack: no dobra, dzieki