Monotoniczność i ekstrema funkcji Michał: f(x) = e^x / x²

Janek191: Na początek oblicz f '(x)

Janek191: Df = ℛ \ { 0}

Michał: f'(x) = e^x*x²−e^x*2x / x⁴ = e^x(x²−2x) / x 4 f'(x) = 0 <=> x²−2x = 0 <=> x = 2 ?

Janek191:

	ex* x2 − ex *2 x		x* ex −2 ex		ex*(x − 2)
f '(x) =		=		=		= 0 ⇔ x = 2
	x4		x3		x3

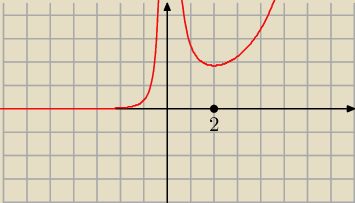
Janek191: Dla x ∊ ( 0, 2 ) jest f '(x) < 0 − f maleje Dla x < 0 jest f '(x) > 0 − f rośnie Dla x > 2 jest f '(x) > 0 Funkcja osiąga minimum lokalne dla x = 2