parametr i logarytm Mariusz: Prosze o pomoc w dokończeniu zadania z parametrem i logarytmem. znaleść wartość parametru m dla którego jest jedno rozwiązanie 2log(x+3)=log(mx) założenia x+3>0 x> −3 mx>0 m≠0 (x+3)²=mx x²+6x+9=mx x²+x(6−m)+9=0 i teraz zrobiłem dla Δ=0 Δ= m²−12m Δ= m(m−12) m=0 lub m=12 i m≠0 → m=12 i dalej nie wiem co zrobić, moze ktoś mógłby dac mi jakąś wskazówkę. W odp jest jeszcze przedział od ( −∞, 0) DZIĘKI

Mariusz: ?

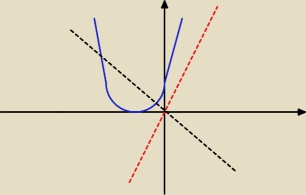
Sabin: Zauważ, że dla m < 0 masz 2 punkty przecięcia, ale jeden z nich (ten bardziej po lewej) nie spełnia założeń co do x (x > −3), w związku z czym tak naprawdę wtedy jest tylko 1 rozwiązanie − to jest ta brakujaca część Twojej odpowiedzi. Na liczbach wydaje mi się że można to zapisać tak: przypadek 1 Δ = 0 − Twoje rozwiązanie przypadek 2. Δ > 0 oraz jeden z pierwiastków ma być < −3 zaś drugi > −3 (zgodnie z rysunkiem) Ponieważ parabola ma łapy do góry, to drugi warunek w tym przypadku załatwia nam wierzchołek, konkretnie f(−3) < 0 z delty masz m < 0 lub m > 12, z drugiego warunku masz że m < 0 co łącznie daje m < 0 i jest brakującą częścią Twojej odpowiedzi.

Mariusz: wielkie dzieki

dona: dlatego ,że : założenie na x jest x> −3 i x≠0 i m≠0 bo mx >0 to: m*x >0 dla x€( −3,0) i m<0 => m€(−∞,0) a dla x€( 0,∞) i m>0 tu : ( m= 12)

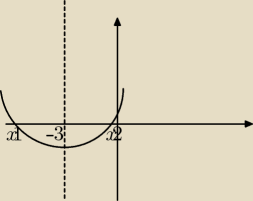
Sabin: Tfu, żadne 'zgodnie z rysunkiem', bo to jest rysunek do rownania (x+3)² = mx Zgodnie z tym rysunkiem (do paraboli x² + x(6−m) + 9):

Mariusz: mam jeszcze takie pytanie. Dlaczego gdy rozpatrujemy x<0 to juz nie rozpatrujemy tej równości ze (x+3)²=mx

Sabin: Nie do końca rozumiem Twoje pytanie. W drugim przypadku (Δ>0) rozpatrujemy funkcję x² + x(6−m) + 9 z dodatkowym warunkiem f(−3)<0. A funkcja ta jest 'konsekwencją' wzoru który podałeś...

Mariusz: czy rzopatrujemy ze zmienionym znakiem m czyli x² + x(6+m) + 9 > 0 tak to wyjdzie ze m∊ (−∞,0) lub (12, +∞) i m<0 m<0

Mariusz: błąd mój

Mariusz: a możesz mi jeszcze wyjaśnić czemu piszemy że f(−3)<0

Sabin: Nie, tu rozpatrujesz normalnie (=0), znak (na >) zmienia się przy delcie i przy warunku f(−3) (na <).

Sabin: f(−3) < 0 załatwia nam to, że miejsca zerowe tej paraboli będą leżały po przeciwnych stronach −3 − i wtedy jedno z nich odrzucimy jako nie spełniające założenia x > − 3, drugie zaś przyjmiemy. Gdybyśmy tam wstawili dowolną liczbę różną od −3, wtedy nie byłoby gwarancji że oba pierwiastki będą leżały po różnych stronach −3. Ale niech mnie ktoś mądrzejszy poprawi jeśli się mylę...

Mariusz: już wszystko jasne, jeszcze raz wielkie dzięki

Sabin: Wrrrrrrrrrrróć! Chrzanię głupoty Nie czytaj tego co napisałem, musi być poprawka

Sabin: A może jednak dobrze... nie wiem, zakręcony dziś jestem jak muszla ślimaka

Sabin: Poprawka na pewno powinna być w pierwszym poście, tam nie powinno być wyrazu 'wierzchołek. Co do reszty, to JEDNAK wydaje mi się że się zgadza

Mariusz: a gdy mamy że ma tylko jedno rozwiazanie ujemne log[(m+4)x]=log(x²+2x) x∊(−∞,−2) lub (0,+∞) (m+4)x=x²+2x x²−x(m+2)=0 x=m+2 i teraz dziel na dziedziny m+2>0 m+2< −2 m> −2 m< −4 i co dalej

Mariusz: gdy m< −4 to przecina w jednym miejscu natomiast gty jest > −2 to funkcja liniowa jest rosnaca i przecina parabolę w dwóch miejscahc. Może być takie uzasadnienie

Sabin: Wydaje mi się, że po prostu możesz to uwzględnić w założeniach. Do warunku na x trzeba dorzucić warunek na drugi logarytm, czyli (m+4)x > 0, czyli m+4 > 0 i x > 0 lub m+4 < 0 i x < 0 (x < −2 po uwzględnieniu innych zał.) Pierwszy warunek nas nie interesuje, bo wtedy rozwiązanie jest dodatnie, zaś drugi, po podstawieniu z Twoich wyliczeń za x = m+2 mówi, że jedno ujemne jest dla m < −4. Ale to znów na chyba jest...