ciąg monotoniczny i ograniczony ktostam: Korzystając z twierdzenia o ciągu monotonicznym i ograniczonym wykaż, że ciąg rekurencyjny jest zbieżny: a₁=1

	an
an+1=2		(2 do potęgi an/3 )
	3

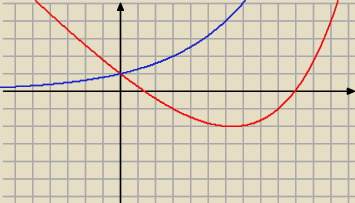Adamm: a_n+1−a_n=2^a_n/3−a_n z rysunku widać że dla danego przedziału ciąg jest rosnący, pytanie tylko czy stale rosnący 1. dla n=1 mamy ³√2−1>0 2. zakładamy że dla n mamy ³√2^a_n−a_n>0 3. ³√2^a_n+1−a_n+1=³√2^3√2a_n−³√2^a_n= =³√2^a_n(³√2^{3√2a_n−a_n}−1)>0 zatem ciąg jest rosnący na mocy indukcji, pozostaje wykazać że jest zbieżny mamy a_n>0 1. a₁<2 2. zakładamy że a_n<2 3. a_n+1=2^a_n/3≤2^2/3<2 zatem na mocy indukcji ciąg jest ograniczony proszę

ktostam: dziękuję