Łatwe zadanie Matematy 30648: W trójkącie ABC dane są AB = 8, BC = 6, AC = 4. Na boku AB obrano punkt D taki że CD=AC. Oblicz pole trójkąta ADC.

Eta:

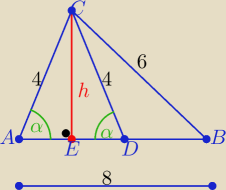
	42+82−62		11
Z tw. kosinusów cosα=		=
	2*4*8		16

	1		11
to |AC|=16k i |AE|=11k ⇒ 16k=4 ⇒ k=		to |AE|=
	4		4

	11		3√15
h=√42−(		)2= ..=
	4		4

P(ADC)= |AE|*h= ..............

Eta: Jak "łatwe" ? to.......... przepisał i poszedł sobie na ...

5-latek: Pozdrawiam