monotonicznosc ktostam: Zbadaj monotoniczność ciągu n²−2n Jak to wykonac? Ciąg jest malejący od n=3.

cosinusx: Ten ciąg nie jest malejący

ktostam: przepraszam, miało być 2ⁿ a nie 2n

ktostam: ale fakt, i tak monotonicznosc wyglada inaczej niz napisałem

Jerzy: Ten ciąg jest stale rosnący.

cosinusx: Nie, jeśli jest tam 2ⁿ zamiast 2n, to nie jest stale rosnący.

Jerzy: Napisałem to przed poprawką autora.

cosinusx: Rozpisz sobie wyraz a_n+1 i odejmij od niego a_n.

ktostam: zrobiłem tak, wychodzi −2ⁿ+2n+1 widać wyraźnie co sie dzieje, lecz nie wiem jak to sprecyzować

cosinusx: No i daj np. "<0", czyli badasz, kiedy malejący.

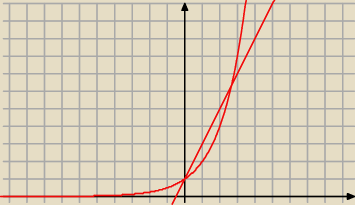
Adamm: n²−2ⁿ=a_n a_n+1−a_n=2n+1−2ⁿ rysujemy sobie 2x+1 oraz 2^x stąd już widać że 2n+1−2ⁿ<0 dla n≥3 co można wykazać indukcją 1. sprawdzamy dla 3, −1<0 2. zakładamy że 2n+1−2ⁿ<0 dla jakiegoś n≥3 3. stąd 2(n+1)+1−2ⁿ⁺¹=2n+3−2*2ⁿ<2−2ⁿ<0 stąd na mocy indukcji ciąg maleje dla n≥3

cosinusx: Jak sobie przeniesiesz, to otrzymasz 2n+1<2ⁿ. Teraz narysuj wykres obu funkcji. I zobacz dla jakich n wykres 2ⁿ jest nad wykresem 2n+1. Pamiętaj, że n jest naturalne.

ktostam: 2ⁿ >2n+1 zachodzi dla n>3, n∊N ... widać to na wykresach funkcji wykładniczej i prostej y=2n+1 . Zapewne na egzaminie nie wystarczy powiedzieć, że to "widać"

Jerzy: Wyrazy ciagu układają sie na wykresie funkcji: f(x) = −2^x + 2x +1 Zbadaj jej monotoniczność. ( w dziedzinie x ≥ 1)

Adamm: widzę że ja tu jestem niewidoczny...

Jerzy: Nasyć bardziej kolorem "nick"

cosinusx: Tak to już jest, jak się zacznie pisać, a w między czasie ktoś inny da odpowiedź

ktostam: dziekuję Adamm, nie zauwazyłem