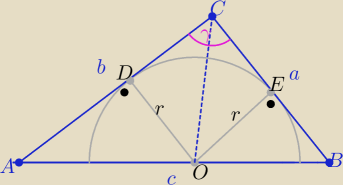
wyznacz promień półokręgu Monika: W trójkącie ABC dane są długości boków AB = 3√2 BC = 3 − √3 oraz AC = 2√3. W ten trójkąt wpisano półokrąg, którego średnica zawiera się w boku AB, styczny do boków AC i BC odpowiednio w punktach D i E. Wyznacz promień tego półokręgu

Eta: c=|AB|=3√2 , b=|AC|=2√3 , a=|BC|=3−√3 Z tw. kosinusów

	a2+b2−c2
cosγ=		=..................... = −1/2 ⇒ γ=120o
	2ab

	√3
sinγ=
	2

	1		1
P(ΔABC)=		*r*b +		*r*a ⇒ 2P=r(a+b) =r(3+√3)
	2		2

	1		√3
P(ABC)=		a*b*sinγ ⇒ 2P= (3−√3)*2√3*		⇒ 2P=3(3−√3)
	2		2

to r(3+√3)=3(3−√3) ⇒ r=................................

Kacper:

Mathmaniac: Dziękuję.

Eta:

Timor i pumba: r= 6−3√3= 3(2−√3) tyle mi wyszlo

Eta: r(3+√3)=3(3−√3) /*(3−√3) 6r=3(3−√3)²⇒ r=3(2−√3) ok

Timor i pumba: Spojrz na tamto zadanie z trapezem jesli mozesz (ciezko idzie

Eta: Sorry... ale nie chce mi się

Timor i pumba: W takim razie ide skoczyc do rowu z woda NIc nie szkodzi , przyjdzie na nie czas