Stereometria endziulla: W ostrosłupie prawidłowym trójkątnym promień okręgu wpisanego w podstawę jest równy 2 cm, a promień okręgu wpisanego w ścianę boczną – 3 cm. Oblicz cosinus kąta nachylenia ściany bocznej ostrosłupa do podstawy. 1. Podstawa − a = 4√3 h = [4√3 * √3] / 2 = 6

Jack: 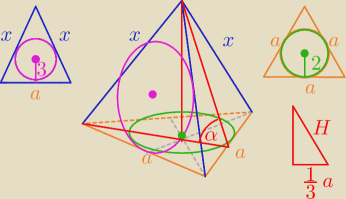====================================================== Podstawa to trojkat rownoboczny (rysunek ten najbardziej po prawej)

	a√3
wys. podstawy : h =
	2

	a2√3
Pole =
	4

	1
Pole z wykorzystaniem okregu =		* 2 * 3a = 3a
	2

a2√3
	= 3a
4

a²√3 = 12a

	12
a√3=12 −−> a =		= 4√3
	√3

	4√3 * √3
h =		= 6
	2

====================================================== ====================================================== Cosinus mozemy znalezc z twierdzenia cosinusow, jednakze potrzebujemy jeszcze wysokosc sciany bocznej. Wiemy jednak, ze promien okregu wpisanego w sciane boczna wynosi 3. (Patrz rysunek po lewej) wysokosc sciany bocznej : H

	1		1
Pole sciany bocznej =		* a * H =		* 4√3 * H = 2√3H
	2		2

	1
Pole z wykorzystaniem okregu : P =		* 3 * (a+2x)
	2

	3
2√3H =		(4√3+2x)
	2

2√3H = 3(2√3+x) 2√3H = 6√3 + 3x 3x = 2√3H − 6√3 = 2√3(H−3)

	2√3(H−3)
x =
	3

z Pitagorasa dla sciany bocznej wykorzystujac jej wysokosc, krawedz boczna i polowe krawedzi pdostawy

	a
x2 = H2 + (		)2
	2

x² = H² + 12 podstawiajac tamtego iksa :

12(H−3)3
	= H2 + 12
9

4		3
	(H2 − 6H + 9) = H2 + 12 /*
3		4

	3
H2 − 6H + 9 =		H2 + 9
	4

1
	H2 − 6H = 0
4

	1
H(		H − 6) = 0
	4

H = 0 (sprzeczne) lub H = 6 * 4 = 24 zatem mamy wysokosc sciany bocznej. oraz krawedz sciany bocznej : x = √ H² + 12 = √588 = 7√12 = 14√3 ====================================================== No i teraz z tw. cosinusow : albo nie...latwiej po prostu obliczyc cosinus alfa i tyle (patrz trojkat na dole po prawej)

	1   * wysokosc podstawy 3
cos α =
	wysokosc sciany bocznej

	1   * 6 3		2		1
cos α =		=		=
	24		24		12

====================

endziulla: Odpowiedź zgodna z odpowiedzią w książce: dziękuję za pomoc!

Metis: Chciało Ci się?

Jack: z kazdym zadaniem coraz mniej (odnosnie planimetrii, stereometrii i geometrii)

Jolanta: Dobrze,że komuś się chce .Też robiłam ale się pomyliłam i dzięki Tobie znalazłam błąd

Metis: Szacunek

Kacper: No przepisanie za przepisanie tego to należy się

Ajtek: Ja bym powiedział, że nawet . Witam Niewitanych .

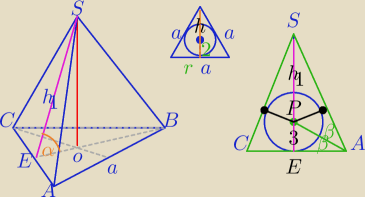
Mila: 1) h=3*2=6, a=4√3 |EO|=2

	|EO|
cosα=
	SE|

2) w ΔPEA:

	3
tgβ=
	2√3

	2*tgβ		3   2*   2√3		3
tg(2β)=		=		=		*4=4√3
	1−tg2β		1−912		√3

WΔSEA:

	h1
tg(2β)=
	2√3

h₁=2√3*4√3=24 3)

	2		1
cosα=		=
	24		12

===============

Jack: ah te kąty

Mila: Czasem ułatwiają, a czasem komplikują.

Jolanta: Witaj .Aż miło patrzec jak Ty to robisz

Mila: