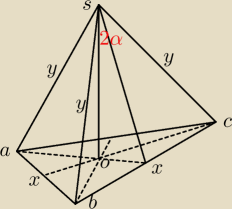
STEREOMETRIA Pati18773: Miara kąta między ramionami ściany bocznej ostrosłupa prawidłowego trójkątnego wynosi 2α. Wyznacz pole powierzchni całkowitej tego ostrosłupa jeśli pole ściany bocznej jest równe S.

	1
S=		y2sin(2α)
	2

	a2√3
Pc=		+3S
	4

Pati18773: nikt nic ?

Kacper: Nie masz odpowiedzi?

Pati18773: Mam i wynosi tyle S(3+√3tgα)

Mila: cd.

	x2√3
PΔABC=
	4

	1
S=		*y2*2 sinα*cosα
	2

	S
S=y2*sinα*cosα⇔y2=
	sinα*cosα

D− środek BC W ΔSDC:

	0.5x
sinα=
	y

x=2y sinα /² x²=4y²*sin²α

	√3		S		√3
PΔABC= 4y2*sin2α*		=4*		*sin2α*		=
	4		sinα*cosα		4

	S√3sinα
=		=S*√3*tgα
	cosα

P_c=3S+S*√3*tgα ============