styczne
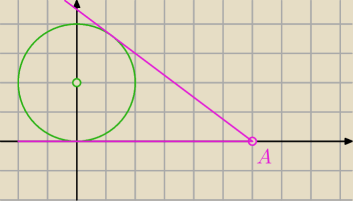
majsa: Z punktu A(6,0) poprowadzono styczne do okręgu x2+y2−4y=0. Oblicz pole figury ograniczonej
tymi prostymi i osiami układu współrzędnych . bardzo proszę o wytłumaczenie
2 sty 14:30
===:
2 sty 14:55
===:
równanie pęku prostych przez punkt A
y=a(x−6)
Podstawiamy do równania okręgu
x
2+a
2(x−6)
2−4a(x−6)=0
x
2+a
2x
2−12a
2x+36a
2−4ax+24a=0
(a
2+1)x
2−4ax(1+3a)+36a
2+24a=0
Styczna ma jeden punkt wspólny z okręgiem ...więc Δ=0
(zauważ, że dla dowolnego a równanie jest kwadratowe)
Δ=16a
2(1+3a)
2−4(a
2+1)(−36a
2+24a)=
= 16a
2+96a
3+144a
4+144a
4−96a
3+144a
2−96a=288a
4+160a
2−96a
itd

2 sty 15:11
===:
oczywiście pomyliłem znak ...ale odnajdziesz pewnie

2 sty 15:20


