równanie kuń: Ile rozwiązań ma równanie 2x³−x²+x+5=0? Myślałem, że zrobię W(x)=0 a potem hornerem, ale nie da się chyba.

kama: pewnie pochodną coś tam, ale ja jestem tępa i nie pomogę

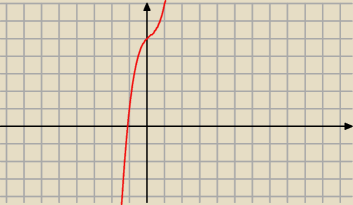
Jack: (1) sposob : Nie pytaja o dokladne rozwiazania, zatem ja bym polecal narysowac przyblizony wykres i wtedy to odczytac. (2) sposob : wykazac ze funkcja jest stale rosnaca, i pokazac, ze jest tylko jedno miejsce zerowe, (pokazac to albo z def. funkcji rosnacej, albo z pochodnej)

Jack: W(x) = 2x³ − x² + x + 5 W'(x) = 6x² − 2x + 1 sprawdzamy, kiedy funkcja W(x) jest rosnaca, tzn. W'(x) > 0 6x² − 2x + 1 > 0 Δ = 4 − 4*6 < 0 zatem ta funkcja przyjmuje wartosci > 0 dla kazdego x ∊ R czyli jest rosnaca. A to chcielismy dowiesc. Skoro jest funkcja rosnaca to ma jedno miejsce zerowe

kuń: dziękuję

Adamm: Jack, dla mnie to trochę błędne rozumowanie sam fakt że funkcja jest rosnąca nie wystarcza żeby powiedzieć że ma miejsce zerowe trzeba jeszcze by powołać się na ciągłość

Adamm: poprawka nie wystarczy ciągłość i monotoniczność, trzeba do tego jeszcze dorzucić punkty w których funkcja przyjmuję różne znaki, na przykład f(0)=5 oraz f(−2)=−17 i teraz dopiero można powiedzieć że z tw. Bolzano−Cauchy'ego istnieje miejsce zerowe pomiędzy punktem −2 a 0, i jest ono jedyne ze względu na to że f jest ściśle rosnąca zatem istnieje jedno tylko rozwiązanie

Jack: Czy nie mozemy stwierdzic ze funkcja, ktora jest ciagla i rosnaca ma na pewno 1 miejsce zerowe?

Adamm: nie, patrz funkcja wykładnicza

Jack: wielomianowa funkcja ciagla i rosnaca. oczywiscie.

Adamm: przecież sam fakt że jest to wielomian 3 stopnia mówi nam że istnieją 1 lub 3 rozwiązania, a ponieważ jest to funkcja rosnąca to musi być jedno, faktycznie ale trzeba o tym wspomnieć

Adamm: raczej, co najmniej jeden pierwiastek, bo mogą być krotne

Mariusz: Funkcja ciągła na przedziale przyjmuje wszystkie wartości pośrednie Policzyć granice na krańcach przedziałów, zbadać monotoniczność, ekstrema sprawdzić wartości w punktach nieciągłości (nie dotyczy wielomianów)

Mariusz: Aby wyeliminować krotne pierwiastki można podzielić przez NWD(W(x),W'(x)) Znamy algorytm kolejnych dzieleń potrzebny do policzenia NWD bez korzystania z rozkładu wielomianu na czynniki