trapez Wiktoria: Rozpatrujemy trapezy równoramienne,w których jedna z podstaw jest 3 razy dłuższa od drugiej oraz suma długości podstaw i wysokości trapezu jest równa 24 cm. a)Wyznacz długości boków trapezu,wiedząc,że jego pole jest rówwne 64cm² b)Wyznacz długości boków trapezu,który ma największe pole.Oblicz te pole Prosze o wytłumaczenie

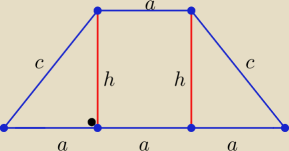
Eta: Z treści zadania: 4a+h=24 ⇒ h= 24−4a , a∊(0,6) i P=2a*h =64 ⇒ a*h=32 a(24−4a)=32 ⇒ a²−6a+8=0 ⇒ (a−2)(a−4)=0 ⇒ a=2 lub a= 4 dla a=2 h=16 to c=√16²+2²= 2√65 dla a= 4 h=8 to c= √8²+4²=4√5 b) h=24−4a P=2a*h ⇒ P(a)=−8a²+48a −−−− parabola ramionami do dołu zatem funkcja pola P(a) osiąga maksimum

	−48
dla amax=		=3 i hmax= 24−4*3= 12
	−16

P_max = P(3)= −8*9+48*3= 72 długość ramion : c=√12²+3²= 3√17