Geometria analityczna
Dawid : W Równoległoboku ABCD dane są A=(−2,−2). C(3,5) oraz BC chodzi o wektor nad BC jest strzałka
[1,4]. Oblicz długość boku DC ,współrzędne środka symetrii równoległoboku ABCD ,pole trojkata
ABC z góry dzikekuje
30 gru 13:58
===:
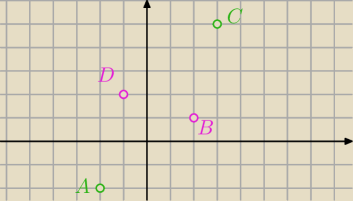
30 gru 14:11
Dawid : Jak obliczyłeś B i D ?
30 gru 14:55
Dawid : I pole trojakta ?
30 gru 15:16
Jerzy:
Masz współrzędne wektora BC→ , więc idziesz od punktu C 4 jednostki w dół i jedną w lewo.
Podobnie od punktu A i wyznaczasz D.
30 gru 15:18
Dawid : Dzięki wielkie tylko tego pola nie umiem zrobić
30 gru 18:22
Mila:
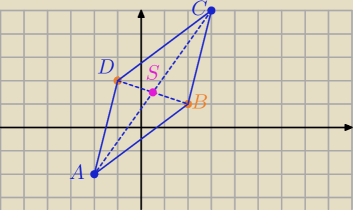
A=(−2,−2), C(3,5)
BC
→=[1,4]
CB
→=[−1,−4]
1)
C=(3,5)→T
[−1,−4]⇒B=(3−1,5−4)=(2,1)
A=(−2,−2)→T
[1,4]⇒D=(−2+1,−2+4)=(−1,2)
2) długość boku DC
D=(−1,2), C=(3,5)
|DC|=
√(3+1)2+(5−2)2=
√16+9=
√25=5
3) S− punkt przecięcia przekątnych− środek symetrii równoległoboku.
Obliczam jako środek DB
| | −1+2 | | 2+1 | | 1 | | 3 | |
S=( |
| , |
| )=( |
| , |
| ) |
| | 2 | | 2 | | 2 | | 2 | |
4) Pole ΔABC:
AB
→=[4,3]
AC
→=[5,7]
4 3
5 7
30 gru 20:20

 A=(−2,−2), C(3,5)
BC→=[1,4]
CB→=[−1,−4]
1)
C=(3,5)→T[−1,−4]⇒B=(3−1,5−4)=(2,1)
A=(−2,−2)→T[1,4]⇒D=(−2+1,−2+4)=(−1,2)
2) długość boku DC
D=(−1,2), C=(3,5)
|DC|=√(3+1)2+(5−2)2=√16+9=√25=5
3) S− punkt przecięcia przekątnych− środek symetrii równoległoboku.
Obliczam jako środek DB
A=(−2,−2), C(3,5)
BC→=[1,4]
CB→=[−1,−4]
1)
C=(3,5)→T[−1,−4]⇒B=(3−1,5−4)=(2,1)
A=(−2,−2)→T[1,4]⇒D=(−2+1,−2+4)=(−1,2)
2) długość boku DC
D=(−1,2), C=(3,5)
|DC|=√(3+1)2+(5−2)2=√16+9=√25=5
3) S− punkt przecięcia przekątnych− środek symetrii równoległoboku.
Obliczam jako środek DB