podstawą ostrosłupa jest romb malinka: Podstawą ostrosłupa jest romb, którego bok ma długość a i a>0. Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod tym samym kątem. Pole jednej ściany bocznej wynosi P i jest dwa razy mniejsze od pola podstawy. Oblicz miarę kąta α nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawy oraz odległość spodka wysokości ostrosłupa od ściany bocznej. Zupełnie nie wiem jak się za to zabrać, proszę o pomoc

Mila: 1)

1		2P
	*a*h=P⇔a*h=2P ⇔h=
2		a

	4a
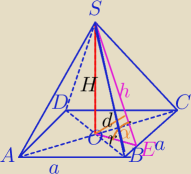
PABCD=		*r=2r*a
	2

2P=2r*a

	P
r=
	a

	|OE|		P   a
cosα=		=
	h		2P   a

	1
cosα=
	2

	π
α=
	3

2) Pole ΔSOE:

	2r*√3
H=		=r√3
	2

	1		1		r2√3		P   ( )2*√3   a
PΔSOE=		*H*|OE|=		*H*r=		=		⇔
	2		2		2		2

	P2*√3
PΔSOE=
	2a2

lub

	1		1		2P
PΔSOE=		*h*d=		*		*d
	2		2		a

P2*√3		P
	=		*d
2a2		a

	P√3
d=
	a

========

Eta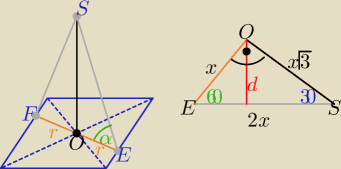: Z treści zadania : P_p=2P

	2P
Pp=a*2r i 2P=a*hb ⇒ a*2r=a*hb ⇒ 2r=hb i hb=
	a

zatem trójkąt EFS jest równoboczny to kąt α= 60^o więc w ΔOES o kątach : 30^o,60^o,90^o

	2P		P		P√3
|ES|= hb=		i |OE|=		i |OS|=
	a		a		a

zatem

	|OE|*|OS|		P√3
d=		= .............. =
	|ES|		2a

malinka: Dziękuję

Kacper: