Oblicz cosinus najmniejszego kąta w tym trójkącie i wysokość na boku BC
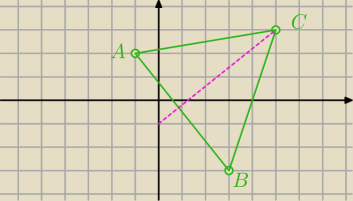
TrVelr: Punkty A(−1,2), B(3,−3), C(5,3) są wierzchołkami trójkąta ABC
a) Oblicz cosinus najmniejszego kąta w tym trójkącie
b) oblicz długość wysokości tego trójkąta poprowadzonej na bok BC
Proszę o pomoc. w a) wiem, że najmniejszy kąt będzie na przeciwko najkrótszego boku. Obliczyłem
długości wszystkich boków. Teraz chyba wystarczy podstawić je do wzoru na cos,
cos=XuXv+YuYv/(|u|*|v|), ale nie wiem jak go zastosować w tym przypadku
co do b) nie mam zielonego pojęcia. Proszę pomóżcie
29 gru 14:23
TrVelr: albo nawet i nie, bo wtedy trzeba by było przeliczać na wektory...
29 gru 14:29
hmm:
a znasz twierdzenie cosinusów

29 gru 14:32
TrVelr: Twierdzisz, że z niego trzeba wyznaczyć ten kąt?
29 gru 14:37
hmm:
29 gru 14:40
hmm:
można różnie

29 gru 14:41
TrVelr: Mógłbyś mi w tym pomóc? Na razie wyliczyłem, że kąt ABC, będzie najmniejszy
29 gru 14:43
hmm:
Jeśli napiszesz równanie prostej przez punkty A i B a potem policzysz odległość punktu C
od tej prostej to masz szukaną wysokość
29 gru 14:43
TrVelr: Wysokość poprowadzona jest na bok BC, czyli jest na odwrót mam rozumieć
29 gru 14:46
hmm:
masz rację to ja pomyliłem
29 gru 14:52
TrVelr: równanie prostej w postaci ogólnej wyszło mi 3x−y−12=0, czyli nawet spoko wynik, ale już
odległość punktu A od boku BC, czyli tej rzekomej wysokości(?) wynosi już −17√10/10
mógłbyś sprawdzić, czy dobrze mi wyszło, bo mam co do tego pewne wątpliwości?
29 gru 14:58
hmm:
OK ... ale bez minusa

zgubiłeś moduł

29 gru 15:00
hmm:
teraz możesz drugim sposobem policzyć cosinus kąta

29 gru 15:01
TrVelr: a co do wyniku to dobry wyszedł? Jeśli nie liczyć tego minusa oczywiście?

29 gru 15:02
hmm:
tak
29 gru 15:03
TrVelr: Okej, a co za drugi sposób do obliczenia tego cosinusa masz na myśli?
29 gru 15:04
hmm:
znając wysokość i |AB| wyznaczysz sinus kąta a znając sinus kąta wyznaczysz jego cosinus
29 gru 15:13
TrVelr: hmmm, czyli w sumie wartość wysokości nam tutaj nic nie daje, albo w zasadzie tylko to, że
tworzy nam trójkąt prostokątny, z którego możemy wyznaczyć różne wartości trygonometryczne.
Jeśli się nie mylę, to trzeba obliczyć połowę odcinka BC i z tego cosinus kąta ABC
29 gru 15:25
hmm:
niby dlaczego
Wysokość jest przyprostokątną ... |AB| przeciwprostokątną ... i to wystarczy
29 gru 15:34
TrVelr: do sinusa tak, ale cosinusa nie. Do obliczenia cosinusa potrzebna jest druga przyprostokątna,
która jest połową boku BC.
A cosinus to właśnie stosunek tej przyprostokątnej do przeciwprostokątnej

29 gru 15:41
TrVelr: może da się to jakoś inaczej obliczyć, ale mi przychodzi do głowy tylko takie rozwiązanie
29 gru 15:42
hmm:
ale przecież potrafisz wyznaczyć wartość cosα znając sinα

29 gru 15:48
TrVelr: z jedynki trygonometrycznej tak? chociaż nie wiem czy ten sposób jest szybszy..
29 gru 15:51
hmm:
dlatego pisałem, że możesz na kilka sposobów... wybór należy do Ciebie

Możesz też Pitagorasem

29 gru 15:54
TrVelr: wtedy musiałbym liczyć sinusa i podstawiać pod ten wzór, a z racji tego, że obliczyłem już
wcześniej długości boków, żeby stwierdzić gdzie znajduje się najmniejszy kąt, mam już długość
boku BC. Tak się składa, że wynosi ona
√40, czyli połowa to
√10, więc wtedy tylko
pozostaje podstawić do stosunku boków i mam już wynik

29 gru 15:56
TrVelr: Dzięki za pomoc, już skończyłem zadanie. Za jakiś czas mogę mieć pytania do kolejnych, także
możesz śledzić moje wątki

29 gru 15:58
Mila:
Punkty A(−1,2), B(3,−3), C(5,3)
|AB|
2=(3+1)
2+(−3−2)
2=16+25=41
|AC|
2=(5+1)
2+(3−2)
2=36+1=37
|BC|
2=(5−3)
2+(3+3)
2=4+36=40
1) Najkrótszy bok to AC, najmniejszy kąt to ∡ABC
z tw. cosinusów:
|AC|
2=|AB|
2+|BC|
2−2*|AB|*|BC|*cosβ⇔
37=41+40−2*
√41*40 cosβ⇔
−44=−2*
√41*4*10 cosβ
2)
prosta BC:
BC
→=[2,6]
| x−3 | | y+3 | |
| = |
| ⇔y=3x−12⇔3x−y−12=0 |
| 2 | | 6 | |
| | |3*(−1)−2−12| | | 17 | | 17√10 | |
d(A=(−1,2),BC)= |
| = |
| = |
| |
| | √32+12 | | √10 | | 10 | |
29 gru 15:59
TrVelr: Ajajaj, faktycznie, można to obliczyć jeszcze chyba z jedynki trygonometrycznej i faktycznie z
twierdzenia cosinusów. Ja nie wiem czemu założyłem, że wysokość dzieli bok na pół, a przecież
nie jest to trójkąt równoboczny, ani nawet równoramienny XD Dzięki chłopaki, co bym ja bez Was
zrobił
29 gru 16:09
cosinusx:
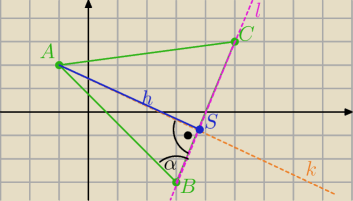
Najmniejszy kąt znajduje się na przeciwko najkrótszego boku.
Liczymy więc długości boków trójkąta:
|AB|=
√41
|AC|=
√37
|BC|=
√40
Zatem najmniejszy kąt znajduje się na przeciwko boku AC, czyli przy wierzchołku B.
Poprowadźmy wysokość tego trójkąta padającą na bok BC w punkcie S.
Niech odcinek BC zawiera się w prostej l, a odcinek AS (czyli wysokość) w prostej k.
Proste te są oczywiście prostopadłe (bo wysokość jest prostopadła).
Wyznaczmy ich równania:
−Prosta l
y=a
lx+b
l
l przechodzi przez punkty B i C, więc za x i y podstawiamy ich współrzędne.
Otrzymujemy układ równań:
−3=3a
l+b
l
3=5a
l+b
l
skąd dostajemy, że a
l=3, a b
l=12.
Zatem równanie prostej l jest postaci: y=3x−12
−Prosta k
y=a
kx+b
k
Ponieważ proste są prostopadłe, to spełniony musi być warunek: a
k*a
l=−1
| | −1 | |
Stąd otrzymujemy, że ak= |
| . |
| | 3 | |
Za x i y podstawiamy współrzędne punktu A, który należy do tej prostej:
| | 4 | |
Skąd dostajemy, że bk= |
| |
| | 3 | |
| | −1 | | 4 | |
Czyli prosta k ma równanie y= |
| x+ |
| |
| | 3 | | 3 | |
Znajdujemy teraz współrzędne punktu S, czy punktu przecięcia się prostych k i l.
Tworzymy układ równań z równań tych prostych.
y=3x−12
Skąd otrzymujemy, że x=4, y=0.
Czyli S=(4,0).
Możemy teraz obliczyć długość wysokości trójkąta, czyli długość odcinka AS.
h=|AS|=
√29
29 gru 16:14
hmm:
no i w ten to oto sposób
Mila została chłopakiem

29 gru 16:17
TrVelr: Musiało nietrafnie skojarzyć mi się z Sebastianem Milą. Najmocniej Panią Milę przepraszam i mam
nadzieję, że moja gafa nie przeszkodzi pomocy mi w kolejnych zadaniach

29 gru 16:23
Mila:

29 gru 16:53
Mila:
cosinusx, masz małą pomyłkę.
29 gru 17:12
cosinusx: Tak, masz rację

głupi błąd rachunkowy

29 gru 22:15



 zgubiłeś moduł
zgubiłeś moduł 




 Możesz też Pitagorasem
Możesz też Pitagorasem 


 Najmniejszy kąt znajduje się na przeciwko najkrótszego boku.
Liczymy więc długości boków trójkąta:
|AB|=√41
|AC|=√37
|BC|=√40
Zatem najmniejszy kąt znajduje się na przeciwko boku AC, czyli przy wierzchołku B.
Poprowadźmy wysokość tego trójkąta padającą na bok BC w punkcie S.
Niech odcinek BC zawiera się w prostej l, a odcinek AS (czyli wysokość) w prostej k.
Proste te są oczywiście prostopadłe (bo wysokość jest prostopadła).
Wyznaczmy ich równania:
−Prosta l
y=alx+bl
l przechodzi przez punkty B i C, więc za x i y podstawiamy ich współrzędne.
Otrzymujemy układ równań:
−3=3al+bl
3=5al+bl
skąd dostajemy, że al=3, a bl=12.
Zatem równanie prostej l jest postaci: y=3x−12
−Prosta k
y=akx+bk
Ponieważ proste są prostopadłe, to spełniony musi być warunek: ak*al=−1
Najmniejszy kąt znajduje się na przeciwko najkrótszego boku.
Liczymy więc długości boków trójkąta:
|AB|=√41
|AC|=√37
|BC|=√40
Zatem najmniejszy kąt znajduje się na przeciwko boku AC, czyli przy wierzchołku B.
Poprowadźmy wysokość tego trójkąta padającą na bok BC w punkcie S.
Niech odcinek BC zawiera się w prostej l, a odcinek AS (czyli wysokość) w prostej k.
Proste te są oczywiście prostopadłe (bo wysokość jest prostopadła).
Wyznaczmy ich równania:
−Prosta l
y=alx+bl
l przechodzi przez punkty B i C, więc za x i y podstawiamy ich współrzędne.
Otrzymujemy układ równań:
−3=3al+bl
3=5al+bl
skąd dostajemy, że al=3, a bl=12.
Zatem równanie prostej l jest postaci: y=3x−12
−Prosta k
y=akx+bk
Ponieważ proste są prostopadłe, to spełniony musi być warunek: ak*al=−1



 głupi błąd rachunkowy
głupi błąd rachunkowy 