znajdź miarę kątów Weronika: W trójkącie ABC, miara kąta ABC jest większa od miary kąta ACB. Odcinek AD leży na dwusiecznej kąta BAC i punkt D leży na boku BC. Punkt E leży na boku BC i jest spodkiem wysokości trójkąta ABC. Wyznacz miarę kąta DAE w zależności od miar kąta ABC i kąta ACB.

Rafal: I w czym problem? Wystarczy odpowiedni rysunek i trochę liczenia kątów.

Weronika: Cieszę się, że dla Ciebie to takie proste. Jednak jakbym miała pomysł na to zadanie to bym go tu nie zapisywała.

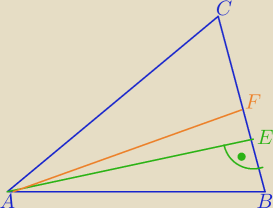
Rafal: Problem może być jedynie z konfiguracją. Jeśli kąt ABC ma miarę większą od kąta ACB, to bok AC jest dłuższy od boku AB. Z twierdzenia Pitagorasa można intuicyjnie stwierdzić, że CE>EB (choć to nie ma większego znaczenia, ale warto wiedzieć). Najważniejsze jest, że

	1		1		1
∡BAF=		∡BAC=		(180−∡ABC−∡ACB)>		(180−2∡ABC)=90−∡ABC=∡BAE, czyli punkt F leży
	2		2		2

pomiędzy punktami C i E.

Weronika: Dziękuje

Rafal: Aha, pomyliłem oznaczenia (F to D),

Rafal: To jeszcze nie koniec Uzależnij miarę kąta DAB od kątów ABC i ACB, a potem miarę kąta EAB od kąta ABC. Potem zauważ, że ∡DAE =∡DAB−EAB.