Wyznacz pole trójkąta BMD. matematyka moja pasja: Punkty D i E są położone odpowiednio na bokach BC i CA trójkąta ABC, w taki sposób,że ^BD_DC=1,5 i ^AE_EC=0,75. Odcinki AD i BE przecinają się w punkcie M, Wiedząc, że [ABC]=1. Wyznacz pole trójkąta BMD.

cosinusx: Wyjaśnij, co oznacza "[ABC]" −pole? obwód?

Matematyka moja pasja: Pole

Rafal: [F] − pole figury F

Kacper: Skoro matematyka to twoja pasja, to może samemu pomyśl

Rafal: Mechanicznie da się to zrobić z twierdzenia Leonarda Cevy − piszemy odpowiednie stosunki pól, (wystarczy wielokrotnie zastosować fakt, że jeśli punkty A, B i C leżą na jednej prostej, to [ABX] : [BCX] = [AB] : [BC], najpierw względem boków, potem względem czewian), rozwiązujemy układ równań i mamy wszystkie pola, o jakie tylko mogą nas zapytać Niestety. nie jest to rozwiązanie ani ładne, ani oryginalne. Może ktoś wymyśli coś ładniejszego.

Rafal: Kacper, wybacz Pisaliśmy w tym samym czasie.

Kacper: Nie szkodzi I tak nie będzie wiedział zapewne o co chodzi Jesteś maturzystą?

Rafal: tak

Kacper: Czyli zapewne olimpijczyk, skoro znasz (w sumie podstawowe) twierdzenia geometrii

Rafal: Niestety, daleko mi do bycia olimpijczykiem

Rafal: Choć zawsze chciałem.

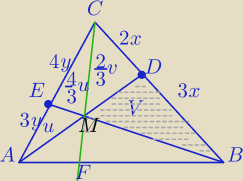
Mila: v, u − pola trójkątów : ΔAME, ΔDMB

	2		2
PΔADC=		PΔABC⇔PΔADC=		*1
	5		5

	4		2		2
(1) u+		u+		v=
	3		3		5

	4
PΔCEB=		PΔABC⇔
	7

	4		2		4
(2)		u+		v+v=
	3		3		7

z (1) i (2) :

7		2		2
	u+		v=
3		3		5

4		5		4
	u+		v=
3		3		7

stąd

	2
u=
	21

	4
v=
	15

Mila: Jak na pasję to mało się interesujesz rozwiązaniami. Chciałabym wiedzieć skąd masz te zadania?

Mila:

Matematyka moja pasja: Od nauczyciela.