geo analityczna
Rafal: Załóżmy, że mam punkty A=(a, 2a), B=(b, 2b), C=(−a−2√3, −2a+√3). Czy zna ktoś jakiś sprytny
sposób na wyznaczenie tych wartości a i b, dla których trójkąt ABC jest równoboczny?
28 gru 16:40
Jack: gdy odleglosci tych punktow od siebie sa rowne, tzn.
|AB| = |BC|
|BC| = |AC|
|AC| = |AB|
albo prostymi.
prosta przechodzaca przez punkty A i B musi byc pod katem 60 stopni do prostej przechodzacej
przez BC i AC.
28 gru 16:47
Jack: nie jest to zaden sprytny sposob... niestety
28 gru 16:48
Rafal: Wszystkie pomysły mile widziane.
28 gru 16:49
Rafal: Po prostu nie wierzę, żeby autor poniższego zadania (z kursu do matury) zmuszał czytelnika do
tak karkołomnych rachunków.
| | √3 | |
Punkt P(−√3, |
| ) jest środkiem boku trójkąta równobocznego. Drugi bok trójkąta leży |
| | 2 | |
na prostej y = 2x. Wyznaczyć współrzędne wszystkich wierzchołków trójkąta i obliczyć
jego pole. Sporządzić rysunek.
28 gru 16:57
Jack: a to musisz poczekac np. na pania
Mile albo
Ete, bo ja to slaby jestem w geometrii

28 gru 17:01
Adamm: może tak
wyznacz proste nachylone do y=2x o 60o, wzorem na tg kąta między prostymi
28 gru 17:02
Adamm: i przechodzące przez P
28 gru 17:02
Jack: akurat to samo mi przyszlo do glowy

28 gru 17:03
Rafal: O, to naprawdę dobry pomysł! Dziękuję.
28 gru 17:04
Rafal: Chyba się poddaje. Policzenie współczynnika kierunkowego, wyrazu wolnego, punktu przecięcia i
jeszcze paru innych rzeczy przy tonie pierwiastków... za słaby na to jestem.
28 gru 17:21
Kacper:

28 gru 17:26
Mila:
Licz tradycyjnie:
|AB|2=|AC|2=|BC|2
28 gru 18:19
Rafal: Nie wierzę w to, co liczę. Mila, czy znasz wynik? Ja dokopałem się do równości 20ab=−15
(nie zdziwię się, jeśli jest błędna), a potem dostałem kosmiczne równanie wielomianowe, o
niecałkowitych współczynnikach do tego.
28 gru 19:04
jc: Wystarczy sobie to wyobrazić. b = −3a, a = √5 /2, o ile sobie to dobrze wyobraziłem.
Sprawdź.
28 gru 19:47
Mila:
Wg moich obliczeń ( raz liczyłam).
lub
Mogę napisać obliczenia, jeśli będziesz miał kłopoty.
28 gru 19:48
Rafal: Dziękuję, wrócę do tego jutro. Dziś nie mam sił.
28 gru 19:53
jc: Na pewno b= − 3a.
Wtedy
(A−B)
2=80 a
2
(A−C)
2 = (B−C)
2 = (2a+2
√3)
2+ (4a−
√3)
2 =20 a
2 + 15
a
2 = 1/4
a= 1/2 lub a=−1/2
Brawo Mila

28 gru 20:06
Mila: a≠b
|AB|
2=(a−b)
2+(2a−2b)
2=(a−b)
2+4*(a−b)
2=5(a−b)
2
|AC|
2=(2a+2
√3)
2+(4a−
√3)
2=4a
2+8
√3a+12+16a
2−8
√3a+3=20a
2+15
|BC|
2=(b+a+2
√3)
2+(2b+a−
√3)
2=
=[(a+b)
2+4
√3*(a+b)+12−(2a+2b)*2
√3+3=
=(a+b)
2+4(a+b)
2+15=5(a+b)
2+15
===========================
5(a−b)
2=5(a+b)
2+15
(*) 5(a−b)
2=20a
2+15
−−−−−−−−−−−−−−
20a
2+15=5(a+b)
2+15⇔
5(a+b)
2=20a
2 /:5
(a+b)
2=4a
2⇔a+b=2a lub a+b=−2a
b=a ∉D lub b=−3a podstawiam do (*)
5*(a+3a)
2=20a
2+15
(4a)
2=4a
2+3
12a
2=3
lub
================
28 gru 20:23
Rafal: Mila

29 gru 08:49
Ale jak: skad wiemy 18:19?
29 gru 10:24
5-latek: Trojkat rownoboczny ma wsztstkie boki rownej dlugosci
We wzorze na dlugosc odcinka masz pierwiastek i zeby sie go pozbyc podnosisz obie strony do
potegi drugiej
29 gru 12:00
Kacper:
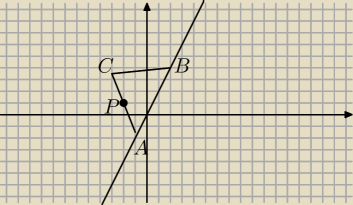
| | √3 | |
Punkt P(−√3, |
| ) jest środkiem boku trójkąta równobocznego. Drugi bok trójkąta leży |
| | 2 | |
na prostej y = 2x. Wyznaczyć współrzędne wszystkich wierzchołków trójkąta i obliczyć jego pole.
Sporządzić rysunek.
np. tak
| | 15 | |
d(P, pr. AB)= |
| , zatem bok trójkąta ma długość 2√5. Liczymy pole. |
| | 2 | |
Kreślimy okrąg o środku w punkcie P i promieniu
√5. Znajdujemy punkt A (układ równań)
Punkt C (środek odcinka) i punkt B (długość odcinka)
Wyniki to:
A=(−0,5; −1)
B=(1,5; 3)
C=(−2
√3+0,5;
√3+1)
P[ABC]=5
√3
29 gru 12:41
jc: To jest zły rysunek.
Wektor (−2√3,√3) jest prostopadły do prostej, na której leży bok AB (prosta ma kierunek
(1,2).
Rzut prostokątny punktu C na prostą AB ma współrzędne (−a, −2a).
Rzut powinien być środkiem odcinka AB.
(−a,−2a) = (1/2) [ (a,2a)+ (b,2b) ]
Stąd b = −3a. A potem podstawimy tak, jak to zrobiłem o 20:06 i mamy wynik.
29 gru 12:55
Rafal: Kacper, co chwila uczę się nowych rzeczy

29 gru 12:56
jc: To nie był zły rysunek, przepraszam.
29 gru 12:57
Kacper:
jc chodzi o mój rysunek? jest niedokładny, bo robiony przed tym jak wykonywane były obliczenia.
29 gru 13:00
Kacper: 
29 gru 13:00
Kacper:
| | √15 | |
Jest literówka, bo odległość punktu P jest równa |
| . |
| | 2 | |
29 gru 13:01
jc: Można było i tak, jak Kacper. P=(1/2)(C+A) =(−√3, √3 /2).
Może po prostu zmyliło mnie oznaczenie P(−√3, √3 /2). Nie potrafię się do tego przekonać.
Czy P(2,3)=P(5,7)? P(3,2)=Q(3,2) ? Bardziej logiczne byłoby oznaczenie (P,2,3).
Wtedy nie mielibyśmy żadnej równości.
29 gru 13:06
Kacper:
jc chodzi ci o zapis? P=(2,3) czy P(2,3)?
29 gru 13:08
jc: Kacper, Twój rysunek jest w porządku

Po prostu pomyślałem o swoim (miałem go tylko w głowie).
U mnie była tylko prosta AB, położenie C dla a=0, oraz prosta równoległa
do AB przechodząca przez C (w przypadku a=0).
29 gru 13:09
jc: P(2,3), lepiej by wyglądało (P,2,3).
29 gru 13:10
jc: P(2,3) wygląda jak wartość P w punkcie (2,3), a nie jak P=(2,3).
Domyślam się, że gdzieniegdzie w szkołach tak uczą. Potem studenci jak widzą
definicję pochodnych mają problem i piszą coś takiego
| | f(x+h)−f(x) | |
iloraz różnicowy |
| |
| | h | |
f(x)=x
2
| | f( (x+h)2 ) − f(x2) | |
iloraz różnicowy = |
| . |
| | h | |
29 gru 13:16
Kacper:
W książkach jest pisane ostatnio jak komu się podoba.
Teraz widzę jest "moda" na stawianie wszędzie kresek np
|∡α| =30o
29 gru 13:27
Kacper:
W 90% podręczników szkolnych występuje zapis P(2,3).
29 gru 13:30
jc: Nie wygląda to ładnie, ale jakiś sens mam: kąt = obiekt geometryczny, |kąt| = miara kąta.
Wolę bez kresek.
29 gru 13:32
jc: W takim razie upierałbym się przy zapisie (P,2,3). Tylko jeden przecinek więcej.
29 gru 13:35
Kacper:
Najgorszy jest brak konsekwencji w uczeniu pewnych zapisów i potem dzieciaki głupieją.
Weźmy takie liczby całkowite (C), a potem student pisze C i dostaje 0 pkt na kolokwium.
Nie wiem jaki problem uczyć oznaczeń międzynarodowych.
29 gru 13:45
jc: Też tego nie rozumiem, to w końcu 5 liter N, Z, Q, R, C. Problem dotyczy Z, Q i C.
Po co się dwa razy uczyć, za każdym razem inaczej?
29 gru 14:18
Kacper:
Ciekaw jestem czy na maturze jak ktoś napisze Z zamiast C uznają.
29 gru 14:27
Li:
Inaczej:
Punkty A i B leżą na prostej :
y=2x
a≠b
| | a+b | |
S=( |
| , a+b)− środek AB |
| | 2 | |
| | 1 | |
s: y=− |
| x+k − symetralna AB, S∊s, na symetralnej leży punkt C⇔ |
| | 2 | |
ustalam wartość k, S∊s
| | 1 | | a+b | | 1 | | 1 | | 5 | | 5 | |
a+b=− |
| * |
| +k⇔a+b=− |
| a− |
| b+k⇔k= |
| a+ |
| b |
| | 2 | | 2 | | 4 | | 4 | | 4 | | 4 | |
C∊s
| | 1 | | 1 | | 5 | |
−2a+√3=− |
| *(−a−2√3)+k⇔−2a+√3= |
| a+√3+k⇔k=− |
| a |
| | 2 | | 2 | | 2 | |
b=−3a
|AB|
2=80a
2
|AC|
2=20a
2+15
−−−−−−−−−−−−−−−−−−−
| | 1 | | 3 | | 1 | |
A=( |
| ,1), B=(− |
| ,−3), C=(− |
| −2√3,−1+√3) |
| | 2 | | 2 | | 2 | |
lub
| | 1 | | 3 | | 1 | |
A=(− |
| ,−1), B=( |
| ,3), C=( |
| −2√3,1+√3) |
| | 2 | | 2 | | 2 | |
29 gru 15:29
Mila:
Teraz to narysuj w układzie współrzędnych, tu trudno zaznaczyć dokładnie
wsp. wyrażone liczbami niewymiernymi.
29 gru 15:35






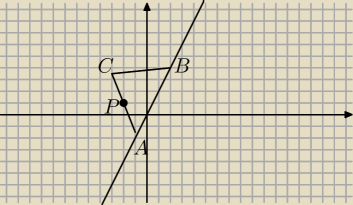


 Po prostu pomyślałem o swoim (miałem go tylko w głowie).
U mnie była tylko prosta AB, położenie C dla a=0, oraz prosta równoległa
do AB przechodząca przez C (w przypadku a=0).
Po prostu pomyślałem o swoim (miałem go tylko w głowie).
U mnie była tylko prosta AB, położenie C dla a=0, oraz prosta równoległa
do AB przechodząca przez C (w przypadku a=0).