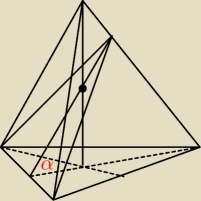
 Przekrój ostrosłupa prawidłowego trójkątnego płaszczyzną zawierającą krawędź podstawy i środek
wysokości ostrosłupa ma pole 2√6. Płaszczyzna przekroju jest nachylona do podstawy pod kątem
45 stopni. Oblicz pole podstawy ostrosłupa.
Przekrój ostrosłupa prawidłowego trójkątnego płaszczyzną zawierającą krawędź podstawy i środek
wysokości ostrosłupa ma pole 2√6. Płaszczyzna przekroju jest nachylona do podstawy pod kątem
45 stopni. Oblicz pole podstawy ostrosłupa.
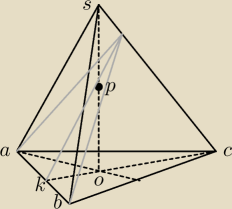
| 1 | a√3 | a√3 | ||||
ko=op= | * | = | ||||
| 3 | 2 | 6 |
| a√6 | ||
kp=ko√2= | ||
| 6 |
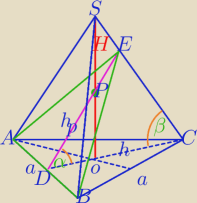 α=45o
DE=hp− wysokość przekroju, OS=H− wysokość ostrosłupa
DC=h− wysokość ΔABC
α=45o
DE=hp− wysokość przekroju, OS=H− wysokość ostrosłupa
DC=h− wysokość ΔABC
| 1 | ||
PΔABE=2√6⇔ | *a*hp=2√6⇔ | |
| 2 |
| a2√3 | ||
PΔABC= | ||
| 4 |
| 1 | ||
|OP|=|DP|= | h | |
| 3 |
| 2 | ||
H=2*|OP|= | h⇔ΔSOC− Δprostokątny równoramienny⇒β=45o | |
| 3 |
| a√3 | 3a2 | |||
( | )2=2*hp2⇔2hp2= | ⇔ | ||
| 2 | 4 |
| 3a2 | a√3 | |||
hp2= | ⇔hp= | |||
| 8 | √8 |
| a√3 | ||
a* | =4√6 | |
| √8 |
| a2√3 | |
=4√3=PΔABC | |
| 4 |
| x√2 | ||
3. jeśli KO=x to PS=x i PQ= | ||
| 2 |
| x√2 | ||
4. wysokość przekroju: h=x+ | podstawa przekroju a=2x√3 | |
| 2 |
| a2√3 | 12x2 | |||
pole podstawy: | = | =3x2 | ||
| 4 | 4 |
| x√2 | ||
2x√3*(x+ | })=4√6 | |
| 2 |
| 4√2 | ||
x2= | ||
| 2+√2 |
| 12x2√3 | ||
pole podstawy: | =3x2√3 i 3x2=4 | |
| 4 |