Monotoniczność, ekstrema Adam: Wyznacz przedziały, w których funkcja rośnie (maleje). f(x)=x*√1−x² Będę bardzo wdzięczny jeśli ktoś wytłumaczy mi jak to rozwiązać... Z góry dziękuję.

Janek191: 1 − x² ≥ 0 ⇒ 1 ≥ x² ⇒ x ∊ < − 1, 1> f (x) = x * √1 − x² więc

	−2 x		x2
f '(x) = √1 − x2 + x*		= √1 − x2 −		=
	2 √1 − x2		√1 − x2

	1 − x2 − x2		1 −2 x2
=		=		= 0 ⇔ x = − 0,5√2 lub x = 0,5√2
	√1 − x2		√1 − x2

Dla x ∊ < − 1, −0,5 √2) jest f '(x) < 0 f maleje Dla x ∊ ( 0,5 √2, 1> jest f '(x) < 0 f maleje Dla x ∊ − 0,5√2 ; 0,5√2) jest f '(x) > 0 f rośnie

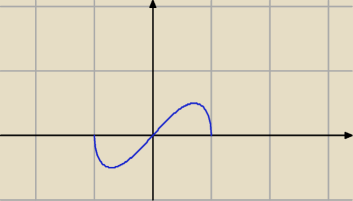
Adamm: ładnie wygląda ta funkcja

Adam: Ech, teraz wszystko jasne... Przy pochodnej trochę się zgubiłem. Wynik się zgadza z odpowiedziami, aczkolwiek mam pytanie dlaczego właśnie w pochodnej w tym momencie ^{1−x2=x/sup>_√1−x2} znika mi w liczniku pierwiastek.

Adam: Coś mi nie wyszło, a chodzi mi o moment odejmowania przy pochodnej w mianowniku 1−x²−x². Serdecznie dziękuję za rozwiązanie zadania