rów. i nierów. żarnik: Rozwiąż: −12x²−x+1<0 oraz x³+x²−9x−9=0 Proszę o jakieś wskazówki w jakiej kolejności sobie z tym poradzić... wiem że jest wiele podobnych przykładów ale ja tego nie potrafię zrobić analogicznie z tymi

Ergo: a znasz wzory na delte i miejsca zerowe?

żarnik: Tak, znam... potrafię je obliczyć. wykorzystać je w nierówności?

Ergo: jesli chodzi o 3 to musisz zauwazyc proporcje miedzy liczbami , albo zauwazyc ze W(1)=0 , czyli 1 jest pierwiastkiem wielomianu i podzielic wielomian przez x−1 lub hornerem. Pozniej. Latwiejszy jest 1 sposob" x³+x²−9x−9=0 x²(x+1)−9(x+1)=0 (x²−9)(x+1)=0 x=3 lub x=−3 lub x=−1

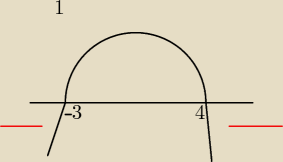
Godzio: tak należy je wykorzystać 1) Δ=1+48 = 49 √Δ=7

	1+7
x1=		= 4
	2

	1−7
x2=		= −3
	2

podaj rozwiązanie 2) x²(x+1) − 9(x+1) =0 (x+1)(x²−9) =0 (x+1)(x−3)(x+3) =0 x=−1 v x=3 v x=−3 jak czegoś nie rozumiesz to pisz

żarnik: mam pytanie... (x2−9)(x+1)=0 możemy zapisać tylko wtedy, gdy w powyższej linijce powtarza się x+1 ? Musi być ten sam znak, tak?

żarnik: mmm... czyli wynik w pierwszy muszę podać zapisany jako przedziały... już rozumiem. Dzięki!

Ergo:

	1		1
godziu zdaje sie ze sie pomyliles miejsca zerowe to		i −		. wspolczynnik a=12
	4		3

Ergo: żarnik można tak powiedzieć. wyłączasz (x+1) przed nawias

Godzio: no rzeczywiście jestem przyzwyczajony że jest x² a nie −12x² sorki za błąd

Godzio:

	8		1
x1=		= −
	−24		3

	−6		1
x2=		=
	−24		4