Pochodna Click: Zbadaj ekstrema lokalne funkcji. Jak postępować z tą wartością bezwzględną ? Pierwszy raz taki przykład robię I x² −5x −6I

Omikron: Sprawdź kiedy funkcja wewnątrz modułu jest dodatnia, kiedy ujemna. Zdejmij moduł w odpowiednich przedziałach, w każdym policz pochodną i poszukaj ekstremów. Na końcu na podstawie wykresu oceń czy w punktach sklejenia tych dwóch funkcji są ekstrema.

Click: To robię. x² −5x −6=(x−6)(x+1) Mam 3 przedziały. Przedziały w których nie zmieniam znaku (−∞,−1) i (6,+∞) Zmieniam znak <−1,6> Nie zmieniony znak pochodna = 2x−5 x=2,5 minimum lokalne Zmieniam znak −2x +5x=0 x=−2,5 maximum, ale nie należy do przedziału. Dobrze ?

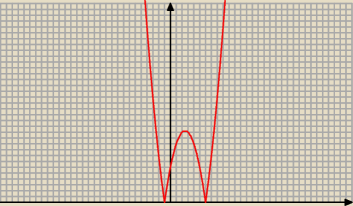
Adamm: chyba nie zrozumiałeś tego co powiedział Omikron, bo dla x=−1 oraz x=6 również mamy ekstrema

Click: Graficznie rozumiem rozwiązanie, tylko jak to obliczyć.

Click: Coś mi świta. Pochodna dla x=1+ x=1−

Adamm: funkcja nie jest różniczkowalna dla x=−1 ani dla x=6, nawet nie musisz próbować funkcja może mieć ekstremum w punkcie x₀ w 2 przypadkach 1. funkcja jest różniczkowalna w punkcie x₀ oraz f'(x₀)=0 2. funkcja nie jest różniczkowalna w punkcie x₀ to jest drugi przypadek to że x=−1, x=6 jest minimum lokalnym jest dosyć proste do udowodnienia dla x=−1 bierzemy bliskie otoczenie, załóżmy przedział (−2;0), teraz w tym przedziale mamy f(−1)=0 oraz f(x)≥0 przy czym jest to jedyna taka wartość, co możemy zobaczyć na przykład z rysunku podobnie z drugim

Adamm: przy czym w pierwszym przypadku funkcja musi mieć ekstremum, w drugim nie

Adamm: nie musi, przepraszam