ttt tade: Boki trójkata prostokątnego ABC mają długość: AC=3, BC=4, AB=5, prosta l, równoległa do prostej AB przecina boki AC i BC odpowiednio w punktach M i N. Niech S oznacza środek odcinka AB oraz MC=x. jak obliczyc pole P(x) trójkąta MNS jaka funkcje zmiennej x (znajdz wzór) prosze o pomoc albo jakies pomysly

www: https://www.matematyka.pl/30809.htm

tade: wlasnie tez znalazlem to ale mam jedno pytanie co do zaleznosci

	3−x		5		5
skąd wiem ze		=		a nie
	h		4		3

tade: bo chyba niewiem czy h jest dluzsza czy krotsza przyprostokątna zeby porownac do tego dużego trojkata?

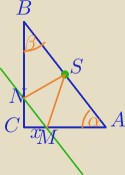
Mila: Możesz obliczyć inaczej− skorzystamy z równoważności pól. W ΔABC:

	4
sinα=
	5

	3
sinβ=
	5

	4
tgα=
	3

W ΔMNC:

	|CN|		|CN|		4
tgα=		⇔		=		⇔
	x		x		3

	4
|CN|=		x
	3

P_ΔABC=6 P_ΔMNS=

	1		4		1		5		4		1		4		5		3
=6−[		*x*		x+		*(3−x)*		*		+		*(4−		x)*		*		]=
	2		3		2		2		5		2		3		2		5

	2
=6−[		x2−2x+6]=
	3

	2
=−		x2+2x
	3

==========

tade: Dzieki mila fajnie rozpisane ale mam jedno pytanie chodzi o pole trójkątów MAS i NSB mianowicie jesli dobrze widze to

	1
liczysz pole		* bok*bok
	2

	1		4		5
np w trojkacie NSB P=		* (4−		x)*		− dlaczego? ten bok jest wysokoscia
	2		3		2

opadajaca na podstawe?

tade: a dobra uzylas wzoru na pole trojkata z dwoma bokami i sinusem kąta miedzy nimi, niezauwazylem, dzieki

Mila:

	1
PΔ=		*a*b*sinα
	2