pole czworokata
wujo: W wypukłym czworokacie mamy AB=3, BC=4, CD=12, DA=13 oraz zchodzi zależność miedzy polami
PACD=5PABC. Oblicz PABCD
25 gru 19:39
Kacper:
Rysunek najpierw.
25 gru 20:40
wjujo:
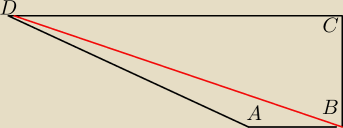
Ok juz i jak dalej
25 gru 20:43
Li:
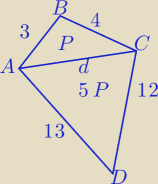
Pole czworokąta:
| | 3+4+d | | d | | 7 | |
p1= |
| = |
| + |
| połowa obwodu ΔABC |
| | 2 | | 2 | | 2 | |
| | 13+12+d | | d | | 25 | |
p= |
| = |
| + |
| połowa obwodu ΔACD |
| | 2 | | 2 | | 2 | |
Pola Δ− wzór Herona
P
ΔABC=
√(d2+72)*(d2+72−3)*(d2+72−4)(d2+72−d)=
=
√(49/4−d2/4)*(d2/4−1/4)
P
ΔACD=
=
√(d2+252)*(d2+252−12)*(d2+252−13)*(d2+252−d)=
=
√625/4−d2/4)*(d2/4−1/4)
Porównanie :
5*P
ΔABC= P
ΔACD /
2⇔
| | 49 | | d2 | | 625 | | d2 | |
25*( |
| − |
| )*(d2/4−1/4)=( |
| − |
| )*(d2/4−1/4)⇔ |
| | 4 | | 4 | | 4 | | 4 | |
| | 25*49 | | 25d2 | | 625 | | d2 | |
( |
| − |
| )=( |
| − |
| ) /*4 |
| | 4 | | 4 | | 4 | | 4 | |
1225−25d
2=625−d
2
24d
2=600
d=5
⇔ΔABC− Δprostokątny
5P=30
P
ABCD=36
25 gru 23:28