Geometria i podobieństwo Mikol: Mamy czworokąt ABCD, i tworzymy czworokąt A'B'C'D', przez połączenie środków kolejnych boków. Jaki musi być wyjściowy czworokąt aby oba były podobne? Z tego co wywnioskowałem czworokąt A'B'C'D' zawsze będzie równoległobokiem (wiem to z podobieństwa), czyli żeby oba czworokąty były podobne, wyjściowy również musi być równoległobokiem. No i skala ich podobieństwa będzie równa k=√2. Łatwo możemy wykluczyć szczególne przypadki kiedy czworokąt ABCD jest: A) Rombem (bo A'B'C'D' będzie prostokątem) B) Prostokątem (bo A'B'C'D' będzie rombem) Zostaje kwadrat i wtedy wszystko się zgadza. Domyślam się, że jest to jedyny taki równoległobok. No ale chodziłoby mi o taki bardziej ogólny dowód dla dowolnego równoległoboku. Z góry bardzo dziękuję za pomoc

g: Mi to wystarczy jako dowód − rozpatrzyłeś wszystkie możliwe przypadki.

Mikol: No właśnie nie jest to pełny dowód, bo nie rozpatrzyłem ogólnego przypadku kiedy czworokąt ABCD jest równoległobokiem. Sprawdziłem tylko szczególne przypadki (ABCD to romb, prostokąt i kwadrat). Niestety to nie starczy, bo teoretycznie dla równoległoboku ABCD cały czas może istnieć równoległobok A'B'C'D' który byłby do niego podobny. No i właśnie nie wiem jak uzasadnić, że tak nie jest Bo jestem pewny, że to podobieństwo działa jedynie dla kwadratu.

an: "zawsze będzie równoległobokiem"⇒ bo boki A'B'C'D' są równoległe do przekątnych ABCD Sprawdź dla równoległboku, w którym przekątna jest równa a√2 i zobaszysz A'B'C'D' podobny będący odbiciem lustrzanym ABCD

Mikol: Nie za bardzo cię rozumiem. No i poza tym nijak się to ma do uzasadnienia, że WYŁĄCZNIE kwadrat jest takim równoległobokiem.

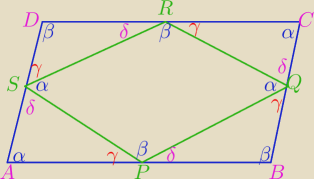
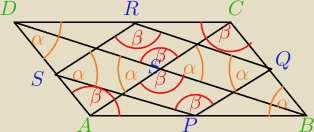
Rafal: Załóżmy, że równoległoboki ABCD i PQRS są podobne (P, Q, R i S to środki boków). Wtedy zachodzą pokazane na rysunku równości kątów o miarach α i β. Spróbuj uzasadnić równości kątów o miarach γ i δ (skorzystaj z faktu, że suma miar kątów w trójkącie wynosi 180, tyle też wynosi suma miar pewnych kątów przyległych). Jeśli ci się uda, to z podobieństwa odpowiednich trójkątów wywnioskujesz, że α=β, a to jest możliwe tylko wtedy, gdy α=β=90. Potem wystarczy uzasadnić, że prostokąt ABCD musi być kwadratem, a potem że kwadrat ma żądaną własność.

Mikol: Super tłumaczenie Wszystko się zgadza

an:

	a
∡ASB=α ∡ABC=β ∡SCB=γ AB=a AC=√2 a AS=SB=
	√2

Wystarczy udowodnić, że α=β to kąty równoległoboku ABCD są równe kątom równoległoboku A'B'C'D' z tw sinusów

a√2		a
	=
sinβ		sinγ

a		a   √2
	=		dzielimy stronami i otrzymujemy
sinα		sinγ

sinα=sinβ czyli każdy równoległobok ABCD jak na rysunku psiadający jedną przekątną równą √2 boku będzie miał takie same kąty jak A'B'C'D' więc nie tylko kwadrat

Rafal:

	AB
Jeśli AS=SB=		, to trójkąt ASB jest prostokątnym trójkątem równoramiennym. Po prostym
	√2

rachunku kątów i skorzystaniu z przystawania kilku trójkątów dostajemy, że Twój równoległobok to tak naprawdę kwadrat

an: tam ma być AS=SC=a√2

Rafal: A co z drugą przekątną?

an: Druga przekątna wynika z długości boku BC którego długość wynika z konsatrukcji trójkąta czyli a√2−a∠b∠ a√2+a

an: Można uogólnić

AC		AB
	=
sinβ		sinγ

AB		AS
	=		AC=2*AS
sinα		sin∡SBA

AC*sinα		AB*sin∡SBA
	=
sinβ*AB		1   sinγ* AC   2

Aby Δ ABC i ΔABS były podobne musi być spełnione α=β oraz γ=∡SBA podstawiamy i otrzymujemy AC=√2AB Mamy łącznie z 27 gru 2016 18:49 dowód , że podobieństwo zachodzi dla równoległoboku o przekątnej równej √2a

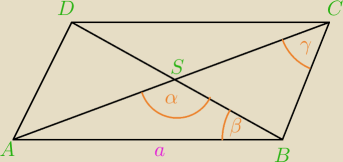
Mikol: an, napisałeś we wcześniejszym poście że z Tw.Sinusów: a/sin(α) = a*√2/sin(γ) No, nie za bardzo widzę z jakiego trójkąta miałoby to wynikać...

Rafal: an, jeśli chcesz, byśmy mogli się odnieść do Twojego rozumowania, musisz konkretnie podać długości boków i przekątnych Twojego równoległoboku. Jeśli boki mają długości a i b, to ile mają dwie przekątne? Poza tym zauważ, że nasz rozumowanie (moje i Mikol) działa także dla Twojego równoległoboku.

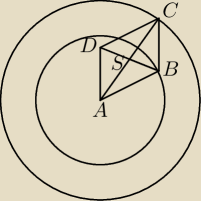
an: W moim rozwiązaniu mieści się równiez kwadrat, ale jest to jedyny prostokąt . Po to narysowałem dwa okręgi A środek okręgu B znajduje się w dowolnym punkcie okręgu o promieniu równym długości boku AB natomiast C na dowolnym punkcie okręgu o promieniu AC=√2*AB. (dlugość b=BC określa odległość puktów B i C) Przyjmujesz dowolnej długości AB kreślisz dwa okręgi, A jest środkiem punkty B i C dowolnie niezależnie od siebie, te trzy punktu są wystarczające do wykreślenia równoległoboku i każdy taki równoległobok spełnia warunki zadania można tam znaleść ∞ wiele kwadratów jednak mają te same wymiary. Jeżeli nie rozumiesz co napisałem poprzednio to sprawdź to na rysunku. Czy Wy odniesiecie się do mego rozumowania to Wasza sprawa, dla mnie to rodzaj rozrywki jak np. SUDOKU, ale przyjemniej by było, gdyby przy okazji Ktoś skorzystał.

Rafal: Niestety, nie pojmuję idei rysowania okręgów, skoro wszystko sprowadza się do tego, że jedna przekątna ma być √2 razy dłuższa od któregoś z boków. Podaj konkretne wartości liczbowe opisujące Twój równoległobok, wtedy uwierzę

an: Weź ekierkę i cyrkiel i skonstruj jak opisałem równoległobok, następnie połącz środki zgodnie z zadaniem porównaj kąty otrzymanych równoległoboków. W dzisiejszych czasach łatwiej i dokładniej możesz to wykonać na komputerze w jakimś programie do kreślenia. co do wpisu an:napisałeś we wcześniejszym poście że z Tw.Sinusów: a/sin(α) = a*√2/sin(γ)

	a     √2
popatrz ja napisałem a/sin(α) =
	sin(γ)

Mikol: an, rozumiem twoją idee rysowania równoległoboku na okręgach, ale nie rozumiem z jakiego trójkąta uzyskałeś tą zależność. Ja nie widzę na rysunku żadnego trójkąta do którego można byłoby to napisać. Bo z tego co rozumiem na początku chesz uzasadnić, że α=β oraz γ=∡SBA. A nie do końca rozumiem jak do tego doszedłeś...

Rafal: Dobrze, przyznaję się do błędu. Nie wszystkie równości kątów, o których napisałem, muszą zachodzić. an,

Mikol: No właśnie też chwilętemu to zauważyłem Z podobieństwa nie wynika, że γ = δ...

Rafal: Równość taka nigdy nie musiała zachodzić Problem leży w tym, że nie wszystkie kąty o mierze δ taka miarę faktycznie mają...

Mikol: Teraz jeszcze trochę pomyślałem nad rozwiązaniem i wydaje mi się, że wpadłem na dość proste rozwiązanie: Zakładając że pary kątów tworzonych przez przekątne są równe parom katów wewnętrznych równoległoboku to wtedy czworokąty ABCD i PQRS są podobne. Dowód: Bo z kątów wierchołkowych i naprzemianległych otrzymujemy, że: ∡DSA=∡RSP i ∡CSB=∡PQR (dla α) ∡DSC=∡SRQ i ∡ASB=∡SPQ (dla β) I wtedy kąty ▱PQRS są równe kątom wyjściowego ▱ABCD, czyli są podobne. Czyli aby oba czworokąty były podobne, kąty przy przecięciu przekątnych muszą być równe kątom wewnętrznym wiekszgo równoległoboku. Być może wiąże się to z tym co an pisał o stosunku przekątnej do jednego z boków... Czy myślicie, że to uzasadnienie jest dobre

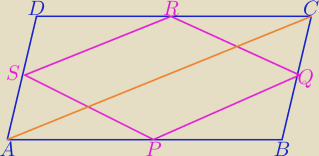
Rafal: Moje (inne) rozwiązanie. Załóżmy, że równoległoboki ABCD i PQRS są podobne (P, Q, R, S to środki boków).

	1
Z podobieństwa trójkątów BPQ i BAC w skali 1:2 wynika, że PQ=		AC.
	2

Z podobieństwa równoległoboków ABCD i PQRS w skali √2:2 (bo pole równoległoboku PQRS to połowa pola równoległoboku ABCD (wystarczy odpowiednio zsumować pola trójkątów narożnych), a stosunek pól figur podobnych to kwadrat odpowiedniej skali podobieństwa) wynika, że

	√2
PQ=		AB.
	2

Wobec tego AC=√2AB. Analogicznie dowodzimy, że BD=√2BC. Czworokąty ABCD o podanych własnościach spełniają warunki zadania.

Rafal: Warto też zauważyć, że jeśli pewna przekątna równoległoboku jest √2 razy większa od pewnego boku, to druga przekątna jest √2 razy większa od drugiego boku (twierdzenie cosinusów). Dlatego konstrukcja an jest poprawna

Rafal: Mikol, to, co piszesz, wydaje mi się rozsądne, tylko pytanie, co z tym dalej zrobisz.

an: cytuję "Czyli aby oba czworokąty były podobne, kąty przecięcia przekątnych muszą być równe kątom wewnętrznym wiekszgo równoległoboku". To jest oczywiste ja do Twojego cytuję "zawsze będzie równoległobokiem" napisłaem⇒ bo boki A'B'C'D' są równoległe do przekątnych ABCD (dodam jaki by on nie był) Boki A'B'C'D' są równoległe do przekątnych ABCD, to przecinająsię pod tymi samymi kątami, jak przekątne ABCD ale to dotyczy każdego czworokata.

Rafal: Ale już fakt, że miary kątów wewnętrznych pokrywają się z miarami kątów przecięcia przekątnych, nie dotyczy każdego równoległoboku...

Mikol: No właśnie miałem podać warunek konieczny i dostateczny na to żeby oba czworokąty były podobne no i wydaje mi się, że ten warunek z kątami w wyjściowym równoległoboku będzie dokładnie taki. Co nie zmienia faktu, że konstrukcja an jest też poprawna. W twoim rozumowaniu warunkiem byłyby stosunki (√2) boków i przekątnych danego równoległoboku. Wydaje mi się, że oba warunki spełniają założenia zadania (tz. konieczny i dostateczny).

Rafal: Też tak uważam, tylko w takiej sytuacji rozumowanie trzeba przeprowadzić w dwie strony.

Rafal: Tak z ciekawości, skąd to zadanie?

Mikol: Matma konkursowa w szkole

Rafal: Fajnie macie, tylko w niektórych szkołach organizuje się kółka konkursowe.

Mikol: No i rzeczywiście zbudowałem taki równoległobok w GeoGebrze (gdzie stosunek boku do przekątnej równy √2) i się zgadza, mniejszy czworokąt jest podobny, oraz jest tak jak mówiłem z kątami przy przekątnych. Bardzo fajne zadanko Śmiesznie się składa, że są dwa takie warunki Dzięki za pomoc an i Rafał

Mikol: an analizowałem twoje rozwiązanie i nie mogę jedynie zrozumieć jednej rzeczy z twojego postu o 27 gru 2016 18:49. Do pierwszej równości (TW.Sinusów) wykorzystujesz △ABC no i tu wszystko jest jasne. Do drugiej równości (TW.Sinusów) o ile dobrze rozumiem wykorzystujesz △ASB, no i z tego co widzę zakładsz, że ∡ABS= ∡ACB=γ. No i wiem, że tak jest (GeoGebra ), ale czy mógłbyś uzasadnić jak do tego doszedłeś? Bo bez tego nie da się uzasadnić, że α=β... A i Rafał zastanawiałem się nad twoim ostatnim rozwiązaniem nie jestem jednak pewien czy działa on również wstecz... No bo uzasadniasz, że jeśli równoległoboki są podobne to mają określony stosunek boków i przekątnych, ale nie wiesz czy na pewno jest tak na odwrót. Czyli jeśli AC=√2AB i BD=√2BC to nie jestem całkowicie pewien czy to implikuje, że równoległoboki są podobne. Niestety jak dokładnie nad czymś pomyślę to zawsze rzeczy komplikuje

Rafal: A czy to nie jest oczywiste?

Rafal:

	√2		√2
Przyjmując AC=√2AB i BD=√2BC mamy PQ=		AB i QR=		BC (podobieństwo w skali
	2		2

1:2)

Rafal: Oczywiście, mowa o podobieństwie trójkątów BPQ i BAC oraz CQR i CBD.

Mikol: Aaa no tak mamy √2PQ=AB i √2QR=BC no i wtedy widzimy, że wszystkie boki obu równoległoboków są proporcjonalne w skali √2. Rzeczywiście dość oczywiste

Mikol: A Rafał mam jeszcze jedno pytanko, już ostatnie Jak pisałeś, że jeśli: "pewna przekątna równoległoboku jest √2 razy większa od pewnego boku, to druga przekątna jest √2 razy większa od drugiego boku (twierdzenie cosinusów)" To mógłbyś to wytłumaczyć, bo ja jakoś tego nie widzę

Rafal: α − miara kąta wewnętrznego a, b − długości boków √2a − jedna przekątna x − druga przekątna 2a²=a²+b²−2abcosα x²=a²+b²−2abcos(180−a)=a²+b²+2abcosα Po dodaniu stronami 2a²+x²=2a²+2b² x²=2b² x=√2b

an: Może to nie jest za ładny ten dowód, nie mniej ∡SAB jest wspólny dla obu trójkątów więc jeżeli zakładamy równoć α=β to z automatu γ=∡ABS jako, że suma kątów w trójkącie wynosi 180^o.

Mikol: No dobra tylko jakoś musisz udowodnić α=β, a z tego c widziałem użyłeś γ=∡ABS w dowodzie... Może się myle ale dla mnie to troche dziwnie wygląda.

an: Mam udowodnić, kiedy te równoległoboki będa podobne a nie, że α=β wykazuję, że wystarczy, aby trójkąty opisane wyżej były podobne Wiadomo, aby trójkąty były podobne musi zachodzić równość dwóch kątów jeden kąt jest wspólny,sprawdzam czy istnieje możliwość,że α=β (co jest równoznacze z równoscia trzech kątów) i otrzymuję odpowiedź że jest to możliwe dla przekątnej równej √2*bok cnw.