kąt goska: W trójkacie równobocznym ABC obieramy punkt wenetrzny P taki ze PA² = PB²+PC² Jak policzyć ∡BPC

Kacper: Rysunek zrób

goska: Ale i tak mi nie wiele pomogło

Rafal: Sprawnie da się to zrobić w sposób analityczny. Wrzucamy ten trójkąt w układ współrzędnych, przyjmujemy, że długość boku to 1 (aby uogólnić wystarczy odpowiednio skalować), stosujemy wzór na odległość między punktami, dość szybko dostajemy równanie okręgu, z którego wynika, że wszystkie punkty P leżą na okręgu o środku w punkcie D i promieniu 1, przy czym czworokąt ABCD to romb. Teraz twierdzenie o kącie wpisanym, środkowym i po zadaniu. Wynik to 150 stopni.

jc: Pięknie

Rafal:

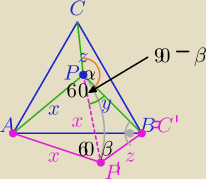
Mila: x²=y²+z² z treści zadania Obracam ΔACP wokół punktu A o kąt 60^o. ΔPBP'− Δprostokątny bo x²=z²+y² ∡P'PB=90−β ∡APC≡∡AP'B=60+β α=360−(60+β+60+90−β)=360−210=150 |∡BPC|=150^o

jc: Jeszcze ładniej, ale za to Rafał podaje wszystkie możliwe położenia punktu P (wartość kąta jest oczywista).

Li: Autora i tak nic to nie interesuje.