ttt tade: zbior T jest zbiorem wszystkich trapezów o obwodzie 60 i kącie ostrym którego sinus wynosi 0.75 znajdz długość ramienia trapezu nalezacego do zbioru T, posiadajacego najwieksze pole w jaki sposob wyznaczyc dlugość ramienia?

Jack: Czy chodzi o trapezy rownoramienne? bo jesli nie to troche malo informacji mamy.

Jack:

	3
sin α =
	4

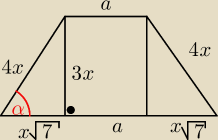
Obwod = a + 4x + x√7 + a + x√7 + 4x = 2a + 8x + 2x√7 Obwod = 60 2a + 8x + 2x√7 = 60 / :2 a + 4x + x√7 = 30 a = 30 − 4x − x√7 wzor na pole :

	1
P =		(a+a+2x√7)* 3x = (a+x√7)*3x
	2

podstawiajac a otrzymujemy P(a) = (30 − 4x − x√7 + x√7) * 3x = (30−4x)*3x = −12x² + 90x Pytanie do tade miales pochodne?

Jack: 1. Jesli miales pochodne no to standardowo pochodna, przyrownanie do zera i mamy ekstremum 2. Jesli nie miales pochodnych no to : PS oczywiscie P(x) = −12x²+90x a nie P(a) zatem mamy P(x) = − 12x² + 90x funkcja ta jest parabola, ramiona skierowane w dol, zatem najwieksza wartosc ma w wierzcholku (bo jest on na samej gorze) czyli liczymy wspolrzedne wierzcholka

	−b		−90		15
p =		=		=
	2a		−24		4

	15
zatem Pole maksymalne uzyskamy dla x =
	4

	15
czyli ramie tego trapezu (skoro wynosi 4x) no to wynosi 4 *		= 15.
	4

Czyli dla ramienia dlugosci 15

tade: dzieki, tak chyba chodzi o trapez rownoramienny bo w odp obwod jest wyrazony jako a+b+2c