zadanie kad:

	x2−4
Naszkicuj wykres funkcji f(x)=log2		.Podaj dziedzinę funkcji i zbiór wartości
	|x|−2

funkcji f. Mi chodzi o zbior

Jerzy: A jaką masz dziedzinę i jak rozpisałeś/aś tą funkcję ?

===:

	x2−4
x≠−2 x≠2		>0
	|x|−2

kad: |x|−2≠0 |x|≠2 x≠2 ∧ x≠−2

Adamm: rozpatruj tylko te wartości dla których x≥0, funkcja jest parzysta więc to bez znaczenia

Adamm:

	x2−4
mamy f(x)=log2		= log2(x+2) dla x>0
	x−2

i teraz log₂(x+2)≥log₂2=1 czyli ZW=<1;∞)

Adamm: miało być x≥0

Adamm: i wykluczamy pewne wartości, a dokładnie x=2 czyli 2∉f(x)

Adamm: a raczej 2∉ZW_f czyli na koniec ZW_f=<1;2)∪(2;∞)

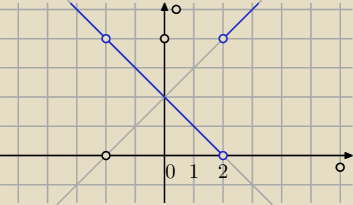
Janek191: x ≠ − 2 i x ≠ 2 Df = ℛ \ { − 2, 2}

	x2 − 4
f(x) =		= 2 − x dla x < 2
	− x − 2

f(x) = U{ x² − 4}[x − 2} = x + 2 dla x > 2 więc ZWf = ( 0, + ∞) \ { 4 } ==================

kad: Mógłbyś to zebrać w jeden post?

Jerzy: Janek ... to jest funkcja logarytmiczna

Janek191: Zrobiłem inne zadanie Gdzieś zgubiłem logarytm

Adamm: bierzemy te wartości dla których x≥0, oczywiście x≠2

	x2−4
wtedy f(x)=log2(		) = log2(x+2)
	x−2

teraz log₂(x+2) jest funkcją rosnącą, zatem najmniejszą wartością jest f(0)=1, musimy też wykluczyć wartość dla x=2, czyli log₂(2+2)=2 zatem ostatecznie ZW_f=<1;2)∪(2;∞)