okregi kajka: wyznacz współrzędne punktów wspólnych dwóch okręgów { x²+y²−10x−4y+7=0 S₁(5,2) r₁ =6 x²+y²−6x−8y+24=0 S₂ ( 3,4 ) r₂=1 jak odejmuje stronami to mi wychodzi 4x+4y−31=0 i jak dalej?

Jack: jak odejmiemy stronami to mamy −4x + 4y − 17 = 0 4x = 4y − 17

	17
x = y −
	4

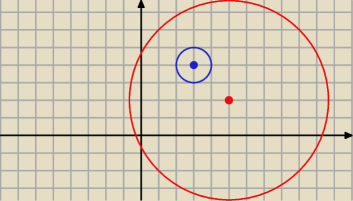
podstawiasz to do dowolnego rownania i rozwiazujesz. przy czym proponuje najpierw (np. graficznie) sprawdzic czy wgl sie one przecinaja.

Jack: a sam uklad rownan to najlepiej tak : mamy rownanie (juz po odjeciu stronami)

	17
−4x + 4y − 17 = 0 a stad mamy x = y −
	4

oraz teraz pomnozmy pierwsze rownanie razy 2 i znowu odejmijmy, wtedy : x² + y² − 14x − 10 = 0 (x−7)² + y² − 59 = 0 wstawiajac tutaj tamtego iksa

	17
(y −		− 7)2 + y2 − 59 = 0
	4

	45
(y −		)2 + y2 − 59 = 0
	4

	45		452
y2 −		y +		+ y2 − 59 = 0
	2		16

	45		1081
2y2 −		y −		= 0
	2		16

delta..

Jack: jest szansa ze cos skopalem.

kajka: w odp ma byc ze nie ma punktów wspólnych

Mila: x²+y²−10x−4y+7=0⇔(x−5)²+(y−2)²=22, S₁(5,2),R=√22 x²+y²−6x−8y+24=0 ⇔(x−3)²+(y−4)²=1, s₂(3,4), r=1 −4x+4y=−17

	17
y=−		+x
	4

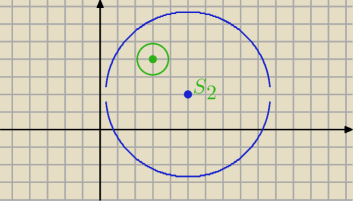
============ |S₁S₂|=√(3−5)²+(4−2)²=√4+4=√8 |R−r|=√22−1 √8<√22−1 okręgi rozłączne wewnętrznie II sposób Podstawienie do równania: (x−3)²+(y−4)²=1

	17
x2−6x+9+(−		+x−4)2=1
	4

	33
x2−6x+8+(x−		)2=0
	4

Otrzymasz Δ<0 brak rozwiązań

Mila: Poprawka: −4x+4y−17=0

	17
y=		+x
	4

	17
x2−6x+9+(x+		−4)2=1
	4

	1
x2−6x+8+(x+		)2=0
	4

	1		1
x2−6x+8+x2+		x+		=0
	2		16

dokończ Δ<0