ciągi Adamm: mając ciąg opisany rekurencyjnie a₀=a, a_n+1=a_n(2−a_n) czy lim_n→∞ a_n = 1 dla a∊(0;2) lim_n→∞ a_n = 0 dla a=0 lub a=2 lim_n→∞ a_n = −∞ dla a_n∊(−∞;0)∪(2;∞) ? dla a∊(0;1) wiem że ciąg jest rosnący i zbieżny do 1, dla a∊(1;2) od drugiego wyrazu mamy 0<a_n<1 zatem ciąg zbieżny do 1, dla a=1 oczywiste, dla a=0 oraz a=2 również, dla a>2 od drugiego wyrazu mamy a_n<0, i ciąg dla a_n<0 jest malejący, a ponieważ nie istnieje skończona granica do której mógłby dążyć (jedyne możliwości to 1 lub 0) to a_n→−∞?

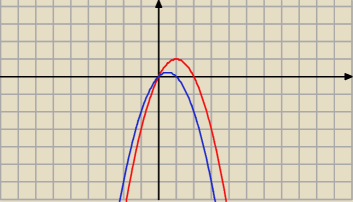
Adamm: z rysunku widać że jeśli a∊(1;2) to ciąg wpada do przedziału (0;1) a wtedy jak już powiedziałem a_n→1, również widać że jeśli a>2 to ciąg wpada do przedziału <0 i wtedy ciąg jest malejący, co również pokazuje rysunek już nie musicie sprawdzać, przekonałem się że jednak moje rozumowanie jest dobre