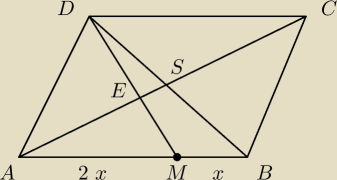
 1/ W równoległoboku ABCD na boku AB obrano punkt M , który podzielił ten bok w stosunku 2:1
licząc od wierzchołka A . Odcinek DM przecina przekątną AC w punkcie E.
Punkt S jest punktem przecięcia przekątnych tego równoległoboku.
Wykaż , że pole trójkąta DES stanowi 5% pola równoległoboku ABCD
2/ W trapezie, w który można wpisać okrąg i na którym można opisać okrąg
wysokość ma długość 8 i kąt ostry trapezu ma miarę 30o
Oblicz długość promienia okręgu opisanego na tym trapezie
1/ W równoległoboku ABCD na boku AB obrano punkt M , który podzielił ten bok w stosunku 2:1
licząc od wierzchołka A . Odcinek DM przecina przekątną AC w punkcie E.
Punkt S jest punktem przecięcia przekątnych tego równoległoboku.
Wykaż , że pole trójkąta DES stanowi 5% pola równoległoboku ABCD
2/ W trapezie, w który można wpisać okrąg i na którym można opisać okrąg
wysokość ma długość 8 i kąt ostry trapezu ma miarę 30o
Oblicz długość promienia okręgu opisanego na tym trapezie

 W piątek znów będę witać Twoje rodzinne miasto
W piątek znów będę witać Twoje rodzinne miasto

| 4 | ||
PAEM= | PDEC | |
| 9 |
| 1 | 1 | 4 | ||||
PADE= | C− | C− | x | |||
| 3 | 9 | 9 |
| 1 | 2 | 4 | |||
C−x= | C− | x | |||
| 4 | 9 | 9 |
| 1 | 5 | ||
C= | x | ||
| 36 | 9 |

| 16√3 | ||
2. ramię tego trapezu wynosi | ||
| 3 |
| 16√3 | 32√3 | |||
wtedy 2a+ | = | |||
| 3 | 3 |
| 8√3 | ||
a= | ||
| 3 |
| 8√3 | 16√3 | 16√3 | 8√3 | ||||
(2r)2=( | )2+( | )2−2 | cos(150o) | ||||
| 3 | 3 | 3 | 3 |
| 16 | 4*16 | 2√3*16 | ||||
r2= | + | + | ||||
| 3 | 3 | 3 |
| 5+2√3 | ||
r2= | *16 | |
| 3 |
| √3 | ||
r=4 | *√5+2√3 | |
| 3 |
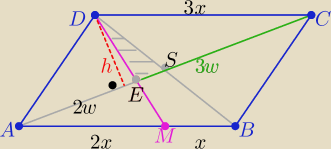 A ja tak :
A ja tak :
| 2 | ||
Z podobieństwa trójkątów AEM i DEC z cechy (kkk) w skali k= | ||
| 3 |
 Ja także
Ja także 


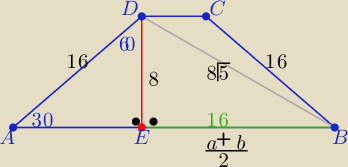 Z treści zadania trapez jest równoramienny o ramionach c=16
.................................
i z twierdzenia sinusów w Δ ABD:
Z treści zadania trapez jest równoramienny o ramionach c=16
.................................
i z twierdzenia sinusów w Δ ABD:
| 8√5 | ||
2R= | ⇒ R=8√5 | |
| sin30o |
