Funkcja logarytmiczna Mike: Dla jakich wartości parametru m równanie ma pierwiastek dodatni? 3+2x=log ¹₃ m Mój wynik to m> ¹₂₇ Mógłby ktoś sprawdzić bo z tyłu książki jest m∊(0: ¹₂₇ )

Adamm:

	log1/3m−3
x=		, m>0
	2

log1/3m−3
	>0
2

log_1/3m>3

	1
log1/3m>log1/3
	27

	1
m<
	27

zgadza się z odpowiedzią w książce funkcja log_ax, a≠1, a>0 jest malejąca dla a∊(0;1)

Mike: Czemu zmienia się znak nierówności?

Adamm: masz odpowiedź na dole, funkcja log_1/3x jest malejąca

Mike: Tzn żeby zachodziła nierówność log ¹₃ m > log ¹₃ ¹₂₇ to musi być m< 1/27 bo gdyby było większe to funkcja log ¹₃ m przyjmuje wartości mniejsze od log ¹₃ ¹₂₇ i wtedy naszą nierówność jest sprzeczna?

Mike: ?xd

Adamm: powiedzmy

Mike: To jakie jest konkretne wyjaśnienie tego że zmieniamy znak nierownosci

Adamm: wyjaśnienie jest takie że funkcja log_1/3x jest malejąca

Mike: Szefie ale co w związku z tym.

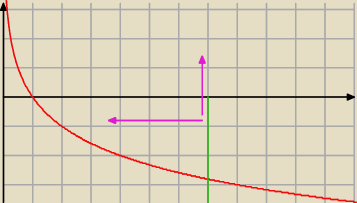
Adamm: czyli jeśli wartość funkcji dla pewnego punktu y jest mniejsza od naszego punktu x, to znaczy to że punktów x musimy szukać po lewej naszego y innymi słowy, log_1/3x>log_1/3y ⇒ x<y

Mike: Moja interpretacja chyba była celniejsza, ale dzięki za konkretną odpowiedź xD

Adamm: nie była celniejsza, była typowa

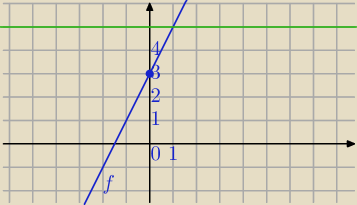
Mila: f(x)=2x+3 y=log_1/3 m, m>0 Równanie : f(x)=log_1/3 m ma dodatnie rozw. dla log_1/3m>3 patrz wykres

	1
log1/3m>log1/3(		)3⇔
	3

	1
m>0 i m<(		)3
	3

	1
m∊(0,		)
	27