Przekroje
Pati18773: Graniastosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź dolnej
podstawy i środki dwóch krawędzi górnej podstawy. Otrzymany przekrój ma pole równe a2. Oblicz
cosinus kąta, jaki płaszczyzna przekroju tworzy z dolną podstawą graniastosłupa.
21 gru 17:37
Janek191:
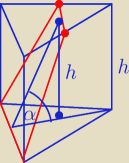
21 gru 19:09
Janek191:
Czy a − długość boku Δ ?
21 gru 19:10
Janek191:
Przekrojem jest trapez równoramienny o podstawach długości a i b = 0,5 a
oraz wysokości h
1
Mamy
0,5*( a + 0,5 a)*h
1 = a
2
0,75 a*h
1 = a
2 / : a
| | a √3 | | a √3 | |
x = 0,5 h2 = 0,5 * |
| = |
| |
| | 2 | | 4 | |
h
2 − wysokość Δ równobocznego
więc
| | x | | 0,25 a √3 | | 3 √3 | |
cos α = |
| = |
| = |
| |
| | h1 | | | | 16 | |
21 gru 19:35
Mila:
Witaj Janku, chyba treść trzeba uzupełnić. Pati pewnie jutro tu spojrzy.
21 gru 20:40
Janek191:
Też mam taką nadzieję

Pozdrowienia dla Mili :

21 gru 21:15

 Pozdrowienia dla Mili :
Pozdrowienia dla Mili : 