Zadanie funkcja kwadratowa - wytłumaczenie esendo: Wykres funkcji kwadratowej f przecina oś Ox w punktach x=1 oraz x=3 i przechodzi przez punkt (0, −3). Wykres ten przesunięto i otrzymano wykres funkcji kwadratowej g(x)=f(x−p). Wierzchołek funkcji g leży na osi Oy. Wyznacz wzór funkcji g. c= −3 b= 4 a= −1 p= 2 q= 1 Wzór funkcji ogólny f(x)=−x² +4x −3 Wzór funkcji kanoniczny f(x)=−(x−2)²+1 Skoro g(x)=f(x−p) to rozumiem, że za x podstawiam (x−2). Wychodzi: g(x)= −((x−2)−2)²+1 g(x)= −(x−4)²+1 g(x)= −x²+8x−15 Moje rozwiązanie jest złe. W internecie jest dobre rozwiązanie, że za x podstawiam x+2, ale nie rozumiem dlaczego skoro p=2

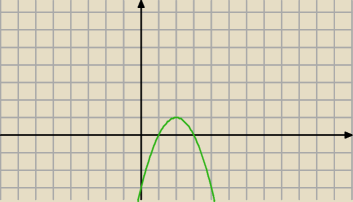
===: Bo treść tego zadania to "panna podpuszczalska" To p w f(x−p) kojarzysz a osią symetrii funkcji f(x) Twoja parabola wyjściowa wygląda jak na wykresie Skoro po przesunięciu f(x) otrzymano g(x) i jej wierzchołek znalazł się na osi 0y ... to znaczy, że f(x) "dostała kopa w lewo o 2" ....czyli g(x)=f(x+2)

Eta: Co to za "język" ? iście matematyczny ?

===: ... a taki tam po pierwszej degustacji tegorocznej "żenichy"

Eta: Jaka wyszła? .... a moja? ... pychota

===: Wyszła super tylko jeszcze nie wyklarowała się całkowicie. Zamiast cukru dodaję miód i nie przegotowuję go jak w niektórych przepisach. Dlatego klarowanie trwa ok 5−6 miesięcy

Eta: Kto by tyle czekał

esendo: Rozumiem. Jedno pytanie jeszcze. Gdyby w zadaniu nie było zdania "Wierzchołek funkcji g leży na osi Oy". Jak należało by to rozwiązać?

===: to w jakiś inny sposób to przesunięcie musiałoby być zdefiniowane