zad tade: wiadomo, ze wykres funkcji f(x)=U{ax²}{(2−x)² ma asymptote pozioma y=2 oraz dla x₀=0 funkcja osiaga ekstremum lokalne. wyznacz wartosc parametru a co tutaj nalezy zrobic?

tade: odpowiedź wyszła mi jak przyrównałem 2 do granicy →∞ tylko wtedy po co byłaby informacja ze osiaga ekstremum dla x₀=0? i zadanie jest za 4punkty wiec cos jeszcze musze zrobic?

Janek191:

	a x2		a
lim		=lim		= a = 2
	4 − 4 x + x2		4x2 − 4x + 1

x→+∞ x→+∞

	2 x2
f(x) =
	(2 − x)2

Janek191: Poprawka; x → −∞

Janek191:

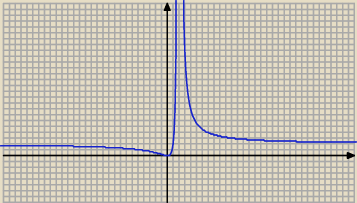
	4 x*( 4 − 4 x + x2) − 2 x2*( 2 x − 4)		8 x
f '(x) =		=		= 0 ⇔
	(2 − x)4		(2 − x)3

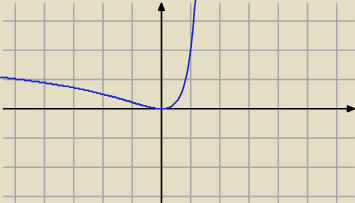
⇔ x = 0 Wykres jest taki

tade: dzieki, to samo mi wyszło tylko zastanawiałem sie czemu tam az 4 punkty sa za jedno obliczenie

Mila: 1) granica 2) Trzeba obliczyć pochodną i sprawdzić, czy przejściu przez x=0 zmienia znak.