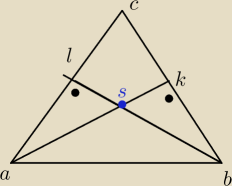
 Odcinki AK i BL są wysokosciami trojkata ABC a punkt S jest punktem ich przeciecia. Uzasadnij,
że okręgi opisane na trójkątach ABC i ABS mają promienie równej długości.
Oczywiscie, że tak będzie, bo ten okrąg opisany na trójkącie ABS i ABC będzie styczny w
punktach A i B, a okrąg styczny do dwóch punktów można narysować tylko w jeden sposób, więc te
promienie będą równej dlugości.
Pytanie− czy taki dowód wystarczy czy coś trzeba jeszcze się pobawić? Szczerze to nie wiem, a w
internetach nie ma rozwiązania tego
Odcinki AK i BL są wysokosciami trojkata ABC a punkt S jest punktem ich przeciecia. Uzasadnij,
że okręgi opisane na trójkątach ABC i ABS mają promienie równej długości.
Oczywiscie, że tak będzie, bo ten okrąg opisany na trójkącie ABS i ABC będzie styczny w
punktach A i B, a okrąg styczny do dwóch punktów można narysować tylko w jeden sposób, więc te
promienie będą równej dlugości.
Pytanie− czy taki dowód wystarczy czy coś trzeba jeszcze się pobawić? Szczerze to nie wiem, a w
internetach nie ma rozwiązania tego
 a nie dowód
a nie dowód





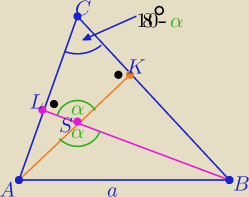 1/ Zapamiętaj ,że wierzchołki oznaczamy wielkimi literami!
Z twierdzenia sinusów w ΔABC i w Δ ABS
R −−− dł. promieni okręgów opisanych na trójkątach ABC i ABS
1/ Zapamiętaj ,że wierzchołki oznaczamy wielkimi literami!
Z twierdzenia sinusów w ΔABC i w Δ ABS
R −−− dł. promieni okręgów opisanych na trójkątach ABC i ABS
| a | a | |||
2R= | = | =.... | ||
| sinα | sin(180o−α) |
 Witam
Witam Moze najpierw zrobilbym konstrukcje zdania czyli skonstruwal te okregi
Wiemy ze srodek okregu opisanego na trojkacie lezy na przecieciu symetrallnych bokow
Potem szukal zaleznosci z wysokoscia
Moze najpierw zrobilbym konstrukcje zdania czyli skonstruwal te okregi
Wiemy ze srodek okregu opisanego na trojkacie lezy na przecieciu symetrallnych bokow
Potem szukal zaleznosci z wysokoscia
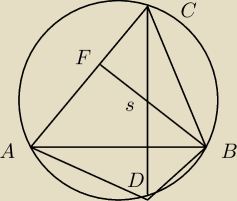 Zrób taki rysunek. AD to prosta zawierająca wysokość trójkąta ABC.
Niech prosta BS będzie odbiciem symetrycznym prostej BD względem AB.
S jest obrazem D.
kąt ACD = kąt ABAD= kąt ABF
Wniosek kąt AFC jest prosty, a więc BF jest wysokością.
Jak odbijesz narysowany okrąg względem prostej AB, otrzymasz okrąg
przechodzący przez ASB. Zatem okręgi z treści zadania mają równe promienie.
Zrób taki rysunek. AD to prosta zawierająca wysokość trójkąta ABC.
Niech prosta BS będzie odbiciem symetrycznym prostej BD względem AB.
S jest obrazem D.
kąt ACD = kąt ABAD= kąt ABF
Wniosek kąt AFC jest prosty, a więc BF jest wysokością.
Jak odbijesz narysowany okrąg względem prostej AB, otrzymasz okrąg
przechodzący przez ASB. Zatem okręgi z treści zadania mają równe promienie.

 1) Okrąg może być styczny do boku.
2) Przez punkt może okrąg przechodzić.
====================
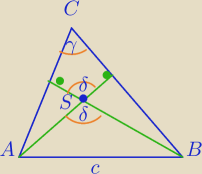
δ=180−γ
W ΔABC z tw. sinusów:
1) Okrąg może być styczny do boku.
2) Przez punkt może okrąg przechodzić.
====================
δ=180−γ
W ΔABC z tw. sinusów:
| c | |
=2R | |
| sinγ |
| c | c | c | ||||
2r= | = | = | =2R⇔ | |||
| sinδ | sin(180−γ) | sinγ |

 Super Wam to wyszło
Super Wam to wyszło  . A i bardzo chętnie oznaczałbym wierzchołki dużymi ltierami, lecz
klikając na symbol "T" nawet z caps lockiem są małe litery.
. A i bardzo chętnie oznaczałbym wierzchołki dużymi ltierami, lecz
klikając na symbol "T" nawet z caps lockiem są małe litery. 

