geometria płaska Mati: Hej mam problem z zadaniami z geometrii, będę wdzięczny za pomoc 1. W trójkącie równoramiennym ABC kąt przy wierzchołku C jest równy 120 stopni. Zakładając, że promień okręgu wpisanego w ten trójkąt wynosi 4−2√3, oblicz pole trójkąta ABC 2. W trapez równoramienny ABCD, AB jest równoległe do CD i AB > DC, wpisano okrąg o promieniu 4. Zakładając, że DC =6, oblicz AB

Janek191: r = 4 − 2√3 Mamy

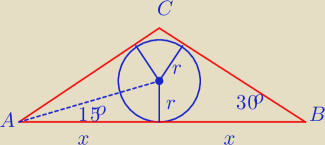
r
	= tg 15o = 2 − √3 ⇒ r = (2 − √3) x
x

	r
x =		= 2
	2 −√3

I AB I = 2*2 = 4

h		√3
	= tg 30o =
x		3

	√3		2
h = x *		=		√3
	3		3

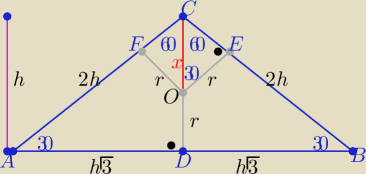Eta: Z własności trójkąta o kątach : 30^o, 60^o, 90^o |AC|=|BC|=2h i |DC|= h= x+r i |DB|=|AD|=h√3

	1
P(ABC)=		*2h*2h*sin120o ⇒ P=h2√3
	2

Z podobieństwa trójkątów : DBC i OEC z cechy (kkk)

r		w		8√3−12
	=		⇒ h=
h√3		2h		3

	2√3
to h= w+r= .... =
	3

P= h²√3=............

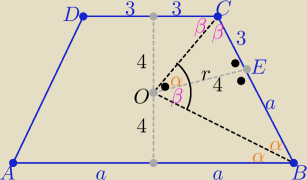Eta: 2α+2β= 180^o ⇒ α+β=90^o zatem trójkąt BOC jest prostokątny |<BOC|=90^o Z podobieństwa trójkątów : BOE i COE

	3		r		16
		=		⇒r2=3*a ⇒ a=		to |AB|=2a=.........
	r		a		3

Mati: Dziękuję bardzo za wszystko

Eta: